图

  1. 相关定义
  • 表示方式 Graph： G（V，E） 由顶点的有穷非空集合和顶点之间的边组成。

线性表的数据元素叫元素，树中叫结点，图中叫顶点Vertex

  • 无向边：两个随机顶点之间的边无方向，用无序偶(Vi,Vj)或(Vj,Vi)表示
  • 有向边：顶点之间的边是有向的，用有序偶表示：<Vi,Vj>表示，与<Vj,Vi>是不同的。 又称为弧。

有向边总是<弧尾，弧头>的。从尾指向头。

  • 简单图：不存在重复边，且不存在指向自身的元素的图。
  • 无向完全图：任意两个顶点都有边,含有n个顶点的图有 n*(n-1) /2的边
  • 有向完全图： 任意两个顶点存在互为相反的两条弧，则为有向完全图，n*(n-1)
  • 稀疏图与稠密图： 边或弧数小于n * logn的图为稀疏图，反之为稠密图
  • 网：图上的边指定权，则称为网。
  • 子图：为父图的子集的图。

2.顶点与边的关系

2.1. 邻接与度

  • 无向图
  • 邻接点：对于G(V,E)，如果边（V1，V2）属于E，则顶点V1,V2为邻接点。

边（V1,V2) 依附 （incident） 于顶点V1,V2 。或说边与顶点V1,V2相关联。

  • 顶点的度（TD）：顶点V的度表示与此顶点相关联的==边的个数==！

  • 有向图

  • 邻接： <V1,V2> 意为V2邻接自V1，V1邻接V2

  • 入度InDegree(ID)：以顶点V2为弧头的称为V2的入度。

  • 出度OutDegree(OD): 以顶点V1为弧尾的称为V1的出度。

  • 总度：TD = ID+OD

2.2 路径
由顶点A到达顶点B

  • 路径的长度：路径上的边的数目
  • 环：第一个顶点到最后一个顶点相同的路径称为回路或环
  • 简单环：除了第一个和最后一个顶点，其他顶点不重复的回路。

2.3 连通图

  • V1V2是连通：如果顶点V1到顶点V2有路径

  • 连通图：任意两个点都是连通

  • 无向图：

  • 极大连通子图（连通分量）的概念：

  • 1.要是子图

  • 2.含有极大顶点数，就是要有此连通子图的极大点数

  • 3.在2的基础上，包含依附于这些顶点所有的边

  • 有向图

  • 强连通图：对于任意顶点的Vi Vj都存在路径。

  • 连通图的生成树：

  • 定义： 一个极小的连通子图，含有所有顶点n，但边只有(n-1)条

  • 有向树：

  • 定义：一个有向图，存在仅有一个顶点入度为0，其他点入度均为1，则为有向树
    有向树

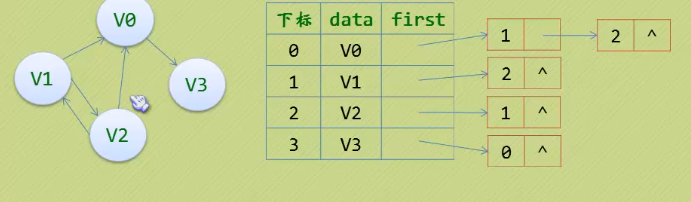
3.存储结构 - 邻接矩阵

内存的物理位置是线性的，但图的元素关系是平面的。

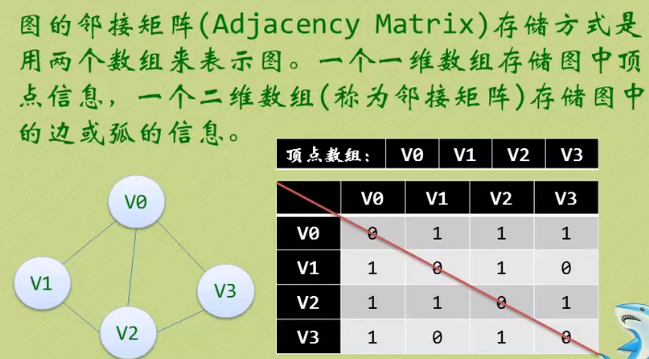
3.1 邻接矩阵（无向图）

  • 存储方式： 顶点用一维数组存储，边、弧用二维数组

  • 无向图的矩阵表是对称的。
    邻接矩阵的存储方式

  • 所谓对称矩阵：就是满足ａ［ｉ］［ｊ］　＝　ａ［ｊ］［ｉ］（０＜＝ｉ，　ｊ＜＝ｎ）。即以对角线为轴，右上角的元与左上角的元是相等的。

  • 有了邻接矩阵的无向图，可以获取以下信息

  • 1.判断两个点是否有边

  • 2.判断一个点的度是多少，只要求某一行某一列的元素之和

  • 3.求一个点的邻接点，获取以点Vi为行或列的一条数组里矩阵值为1的点。

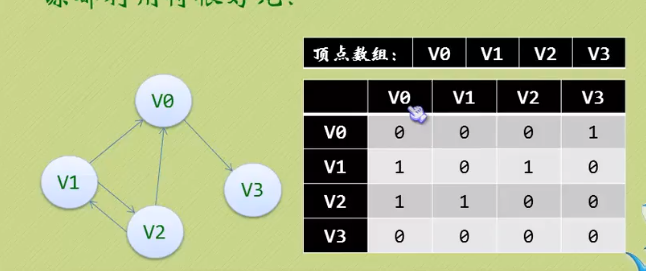
3.2 邻接矩阵（有向图）

有向图的邻接矩阵

  • 特性：
  • 1.有向图的邻接矩阵一般不是对称矩阵，除非所有顶点都互相邻接
  • 2.入度的值即为矩阵的列的各数之和。出度为行的各数之和。

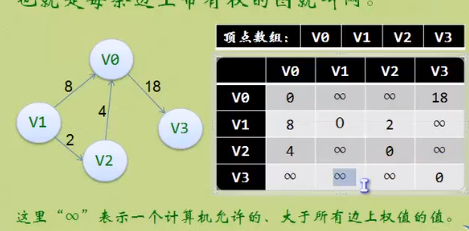
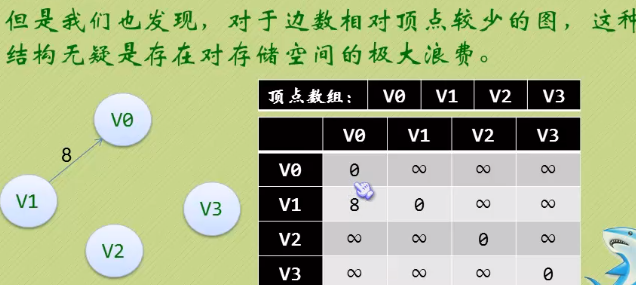
3.3 邻接矩阵（网）

每条边带有权的图就叫网。

  • 即0为自身关联，无穷表示没有弧。

网的邻接矩阵

4.存储结构 - 邻接表

思考

  • 以数组链表的形式存储
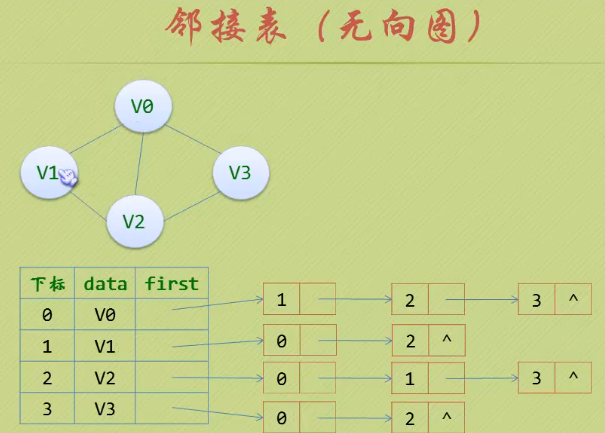
    4.1 无向图
    无向图的邻接表

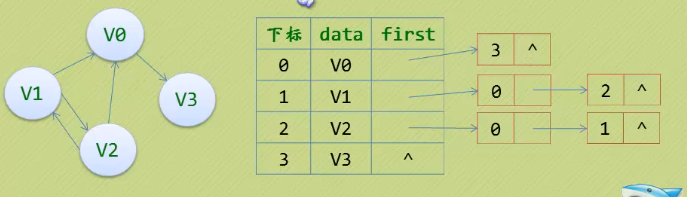
4.2 有向图

  • 以每个点当弧尾建立邻接表。这样更容易得出每个点的出度。
    有向图的邻接表

有向图的逆邻接表
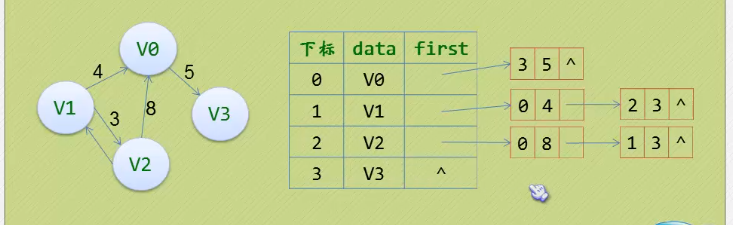
有向图的逆邻接表

4.3 邻接表（网）

  • 区别于有向图，增加一个数据域存储权值

邻接表存储图

  1. 存储结构 - 十字链表

4的邻接表无法满足不同的入度出度都有需求的情况，因此使用新的结构来存放
把邻接表与逆邻接表放在一起

基础结构

十字链表

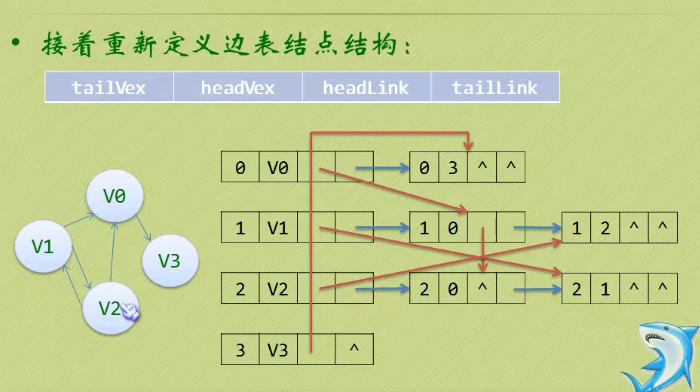
  • 特性：
  • 更容易找到入度与出度
  • 算法复杂度与邻接表是一样，是有向图应用中好用的数据结构

6.存储结构- 邻接多重表

  • 专为无向表设计，边表存放的是一条边，而不是一个顶点

邻接多重表的边表结构

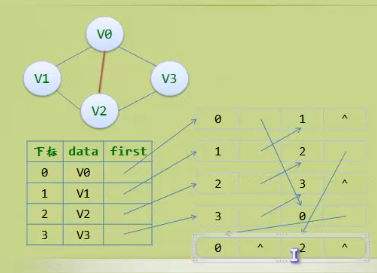
邻接多重表-示例

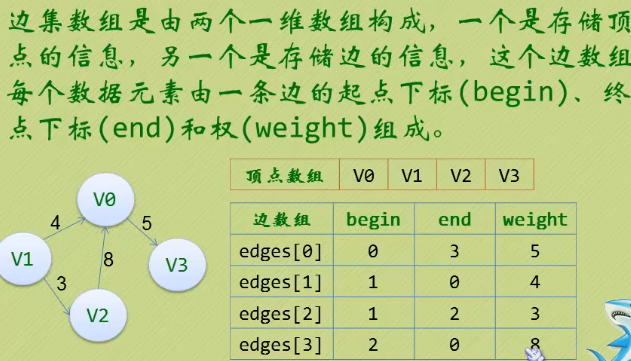
7.存储结构 -边集数组

  • 使用两个一维数组构成，一个存储顶点，一个存储边和权重

边集数组

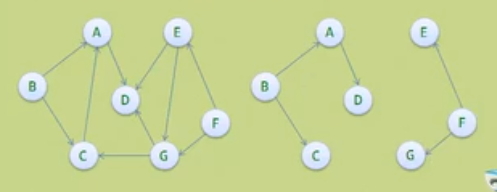
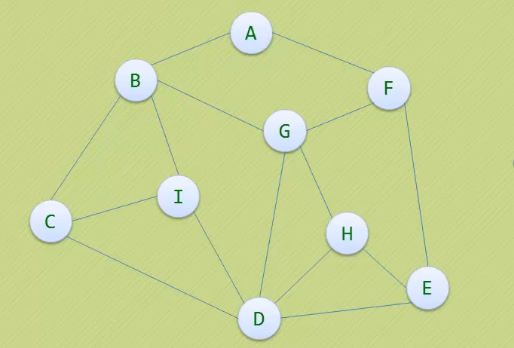
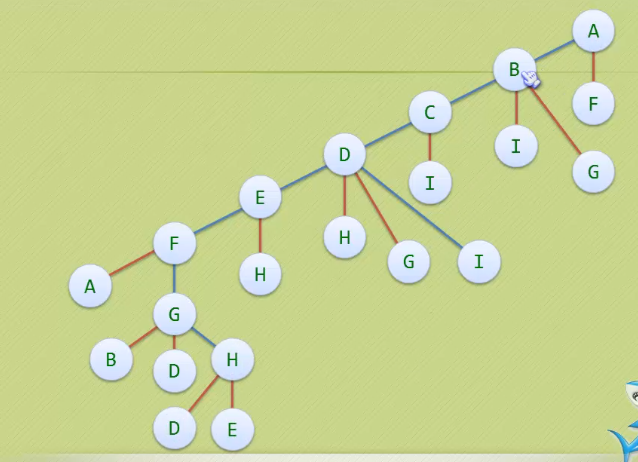
  1. 遍历-深度优先遍历
  • 概述： 以一个点开始，以左/右固定遍历原则来遍历一个图，每成功访问到的一个顶点就标记一下，已经遍历到的点就回退到上一层。以此循环

示例
右手原则的深度优先遍历

. 哈密尔顿路径

  • 经过图中每个顶点且只经过一次
    如果最终还能回到起始点，则称为哈密尔顿回路

扩展-马踏棋盘算法
递归： https://www.cnblogs.com/lpfuture/p/7111524.html
贪心非递归：https://www.jianshu.com/p/6c185f290e10

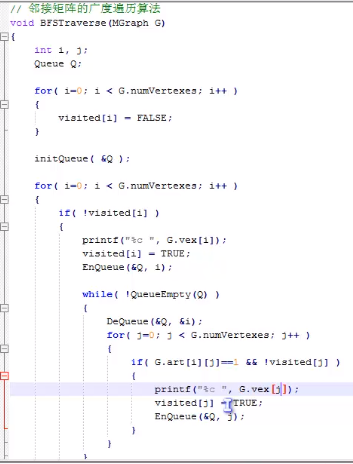
9.遍历-广度优先遍历

  • 类似于树的层级遍历，一层一层遍历
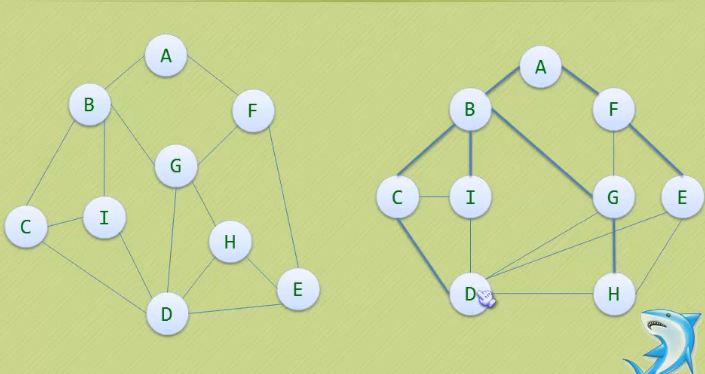
    广度优先遍历

  • 常用实现：使用队列的形式：
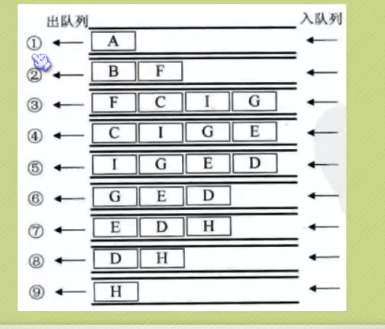
    队列实现广度遍历

算法实现

10.最小生成树 - 普里姆算法：
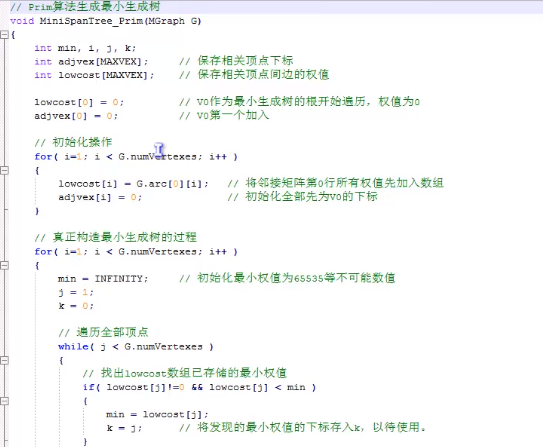
普里姆算法C-Part1

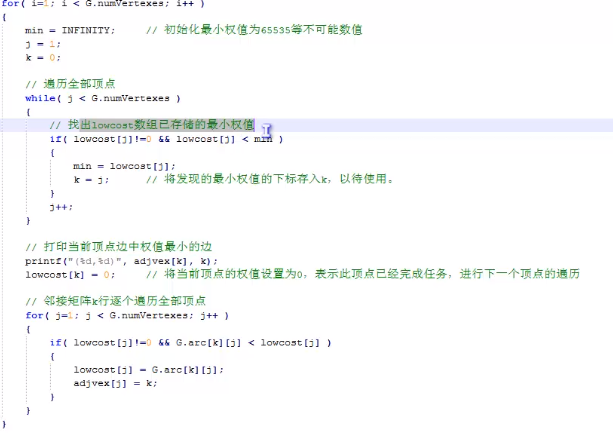
普里姆算法C-Part2

以此文章为示例学习：
https://blog.csdn.net/yeruby/article/details/38615045

从一个点开始以一个数组记录接下来能走的路的权值，下一步的路将是这些权值中的最小值，将将游标移至此最小值的点，标记此点完成状态。接着重复此过程，每次都更新权值数组的值，直到所有的点都被标记为完成。 一定要注意是更新！！！

时间复杂度对比