计算机图形学编程笔记2
一、光线追踪
原理
起因: 光珊化不能很好的处理全局的效果, 如软阴影,较光滑的金属表面(Glossy)反射问题,间接光照(光线多次弹射才进入人眼)
光追的特点:非常慢
光线的假定
- 光沿直线传播(并不正确)
- 光与光不会碰撞(并不正确)
- 光线一定从光源出发最后到达眼睛(reciprocity光线可逆性性质,实际物理上不可逆性)
光追:实则是从相机出发经过不断反射折射到光源,由相机出发,此光线沿着直线,遇到阻挡的物体时点(只记录最近的交点),再判定此点到光线是否是在阴影,不在阴影,这时再进行shading。
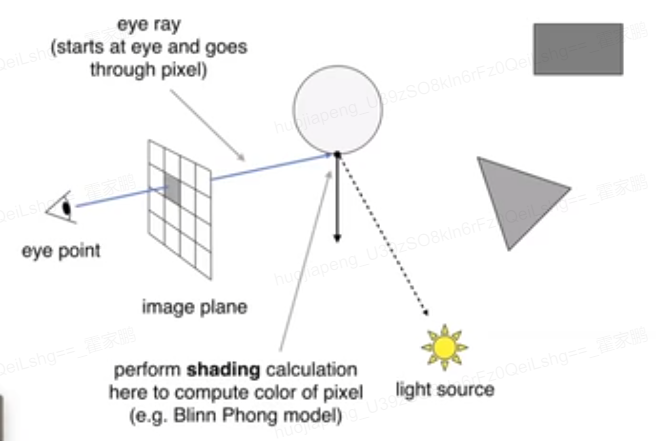
以上其实只考虑了光线弹射一次的情况,那考虑多次弹射时,这时引入一种光追算法: Whitted-Style Ray Tracing
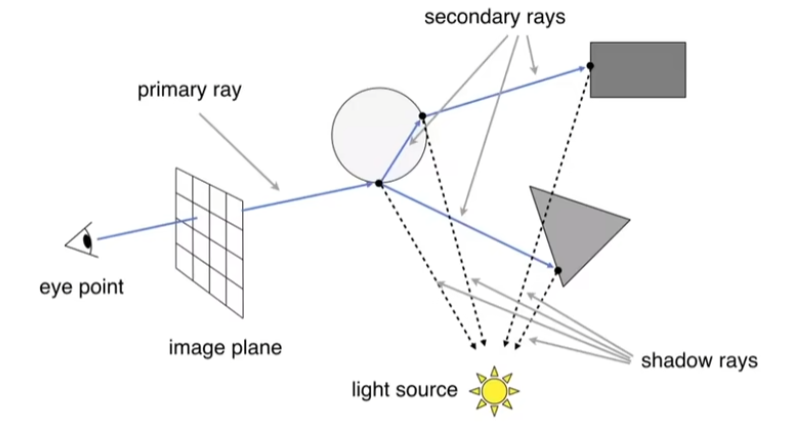
Recursive Whitted-Style Ray Tracing (1979年)
对于每个光线产生的交点,都被计算回到最终的显示。 如中间产生的折射也算在内。
Shadow ray: 表示最终与光线连接需要判断是否要显示的光线
- 求光线射出去的交点:
- Ray Equation:对于光线上的点,都可以表示为以下等式:

- 光线与求交点
对于隐式的图形
p是球上的点

对于这个p,一定两者都满足,得出:
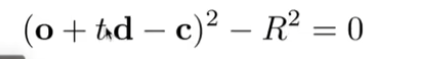
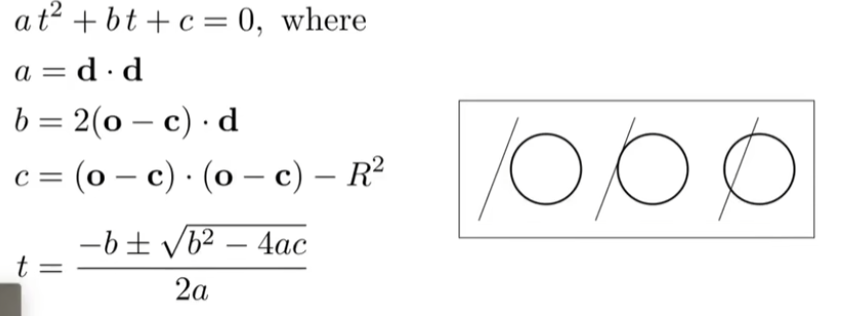
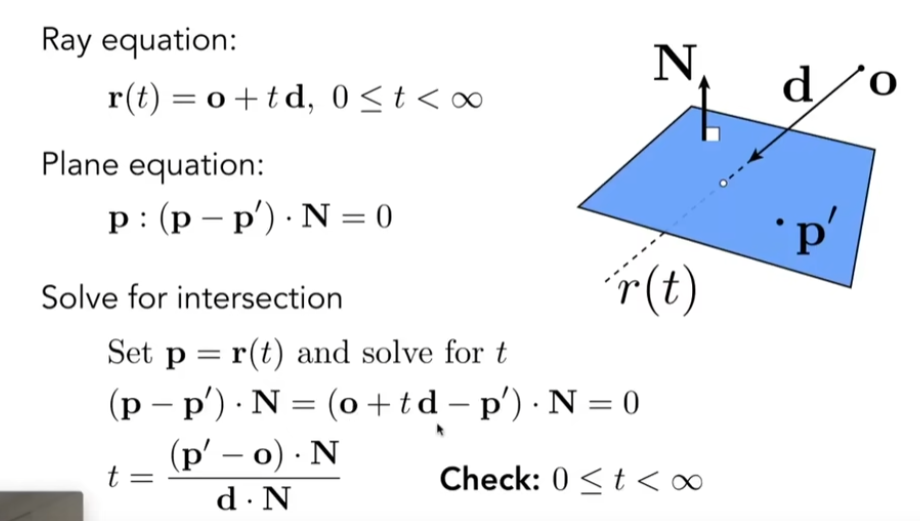
- 对于显式的图形,求光线与三角形的交点
设定光线与三角形必定有0或者1个交点
需要两步: 第一步判断是否在三角形内,第二步判断光线是否与平面有交点
- Ray Equation:对于光线上的点,都可以表示为以下等式:
平面的定义
一系列平面上的点+ 法线
判断点p‘是否在平面上,则 平面上的点p - p’ 与N 一定垂直,点乘必定为0
Moller Trumbore 算法来求光线是否在与平面有交点,使用重点坐标
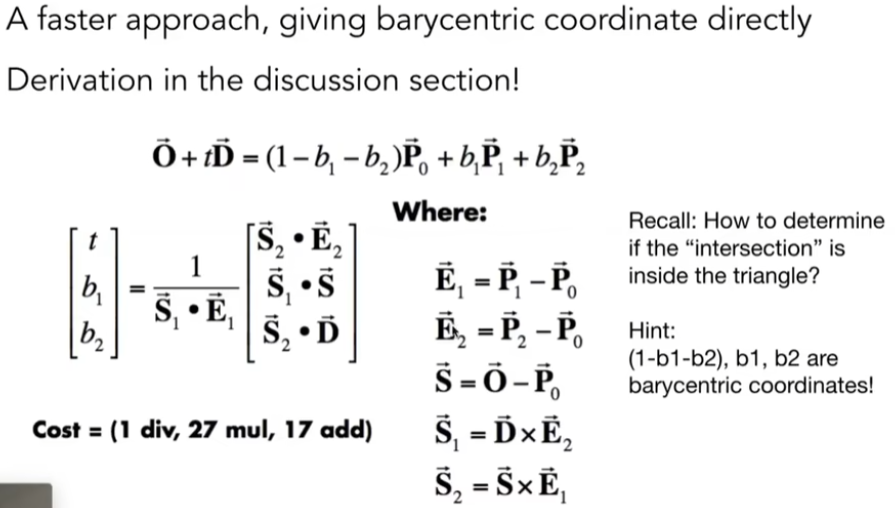
- 由于求交点的过程太缓慢,需要做加速,使用预处理的方法
Bounding Volumes 对得复杂物体,先找出一个包围盒,优先判定光线与包围盒是否有交点,如果没有,直接跳过。
轴对齐包围盒Axis-Aligned Bounding Box AABB
对于三维空间,有三组分别是X,Y,Z对面,当光线进入全部的对面时,则表示光线进入过此包围盒。


那划分的问题?
优先对整个包围盒进行格子划分,先判断与描灰的格子(与物体相交的格子面)的相交(总是认为较快的),再判断与格子内的物体是否有交点
- Spatial Partitions 空间划分
- Oct-Tree 八叉树,对于一块空间切成八块,二维是四块。通过此种方式把空间切成各种结构,但与维度有关,解决此问题使用KD-Tree
- KD-Tree 对于每一层不同的位置或水平垂直方向进行分割,每次拆两次,类似于二叉的分法
- BSP-Tree 每一次选一个方向进行分割,区别于KD-Tree则每个方向不确定性
步骤:
- 做光追之前,优先做出KD-Tree,KD-Tree Preprocessing
数据结构生成:
* 分割坐标系xyz
* 画在哪
* 中间结点的子结点
* 实际物体不存在中间结点,只存在叶子结点。 - 光线来了迭代KD-Tree Traverse KD-Tree
* 与叶子结点有交点,则需要与此叶子结点的所有物体进行比较,找具体的物体的交点
* 与中间结点有交点,找其下的叶子结点再进行比对
KD-Tree的问题:
-
三角面与包围盒相交的情况,三角形与包围盒求交比较困难
-
三角面与多个包围盒相关的情况,则在多个包围盒里都要存同一个三角面
-
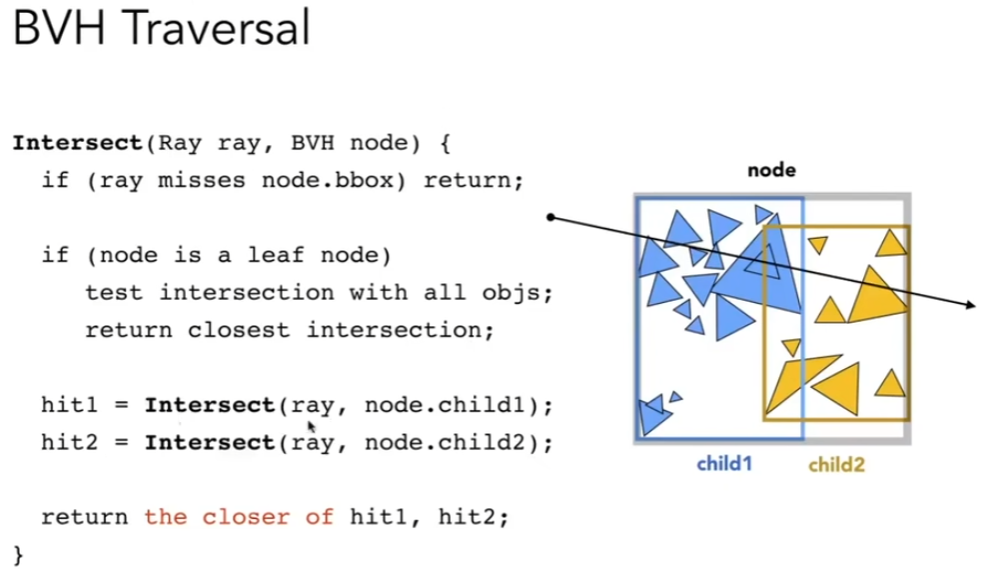
针对KD-Tree的问题的改善的加速结构 - Bounding Volume Hierachy(BVH)
针对物体进行划分,分别求其包围盒。这样解决的KD-Tree的第二个问题。当划分的足够好的情况,也可以避免掉KD-Tree的1问题
递归流程- 找到包围盒
- 把任意包围盒的物体,拆成两部分
- 重新计算包围盒
适当停止,将最终物体放到叶子结点
构建BVHs:
如何切分物体?
- 永远选择一个最长边切割
- 尽可能的构建一个平衡树结构,找到中位的点
停止切分的规则:
Heuristic: 包围盒内物体小于5时
Basic Radiometry 辐射度量学
Whitted Style光追的问题:
光线的强度的单位表示?
物体表面与光的作用真实吗?
辐射度量学给予的:
- 度量系统, 光照的单位
- 精准描述光照, Radiant flux, intensity, irradiance, radiance
- 从物理的基础上准确的显示光照计算
学习方法推荐:
为什么有?-> 是什么?->怎么用?
WHY->WHAT->HOW
-
Radiant Energy and Flux(Power)
Radiant Enery: 光波辐射的能量 Joule 焦尔,很少用在CG中
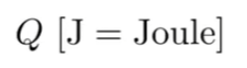
Radiant Flux(Power): 单位时间内产生的能量 Watt 与lumen,Lumen表示光源的亮度,图形学用的
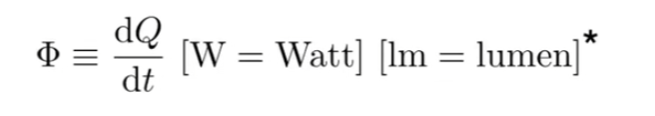
单位时间通过的光子数量 -
Radiant intensity
每个单位立体角(unit solid angle)上的power: power per solid angle
Solid Angle(立体角): 球的立体角:两种除r平方(圆的立体角:弧长除r)三维上对于角度的延伸,任何一个点光源的辐射,如果是一个均匀的发射光源,则可以是各个power的积分除上4 PI。
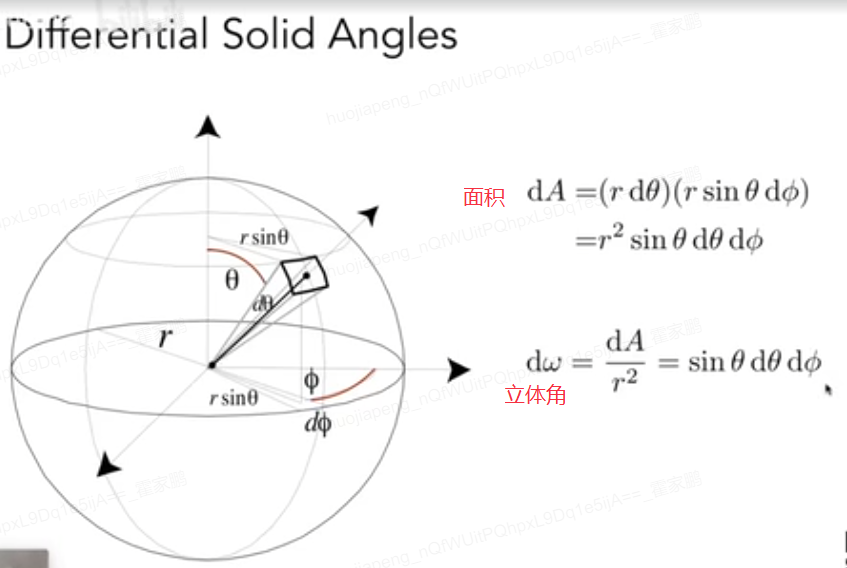
特别地,对于单位球,立体角就是投影到的单体面的面积
-
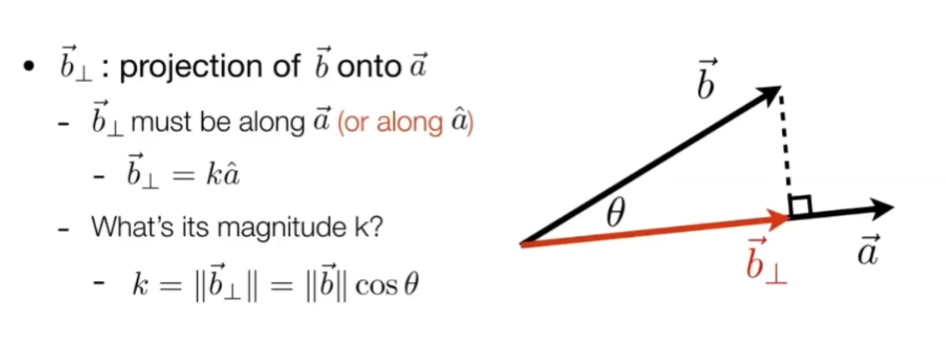
Irradiance: 无方向
每一个面积上对应的power: power per projected unit area
Power per unit area! 能量除去面积. 定义必须面得与光线垂直的面积,其他情况不能算。
图形学上,可以直接理解为一个面上收到的所有的能量 -
Radiance: 有方向
光线的属性,power per unit solid angle, per projected unit area. 单位立体角和单位立体面积微分两次
考虑某一个确定的面,和某一个确定的方向(角),这样就与光线的特征相近。
Incident Radiance = Irradiance per unit solid angle 入射进来。考虑有方向的irradiance。
Exiting Radiance = Intensity per unit solid area 小的面辐射出去,往哪个方向去。
radiance与irradiance关联起来,一个面的所有radiance积分即为irradiance
Bidirectional Reflectance Distribution Function BRDF
一方向的光进来,会往多少不同的方向去反射多少能量。
- BRDF = 任意一个出射方向radiance的微分 / 入射点上的irradiance的微分
某一个面 dE(wi) 的irradiance接收到的光线,就是对应某一个方向L的radiance即公式中表示radiance乘以此方向的立体角。
考虑一个dA微面,在某个方向Wi接收到的irradiance,然后会如何被分配到各个立体角上去,这样的一个比例称为BRDF。 dA出去的radiance / dA收到的Irradiance

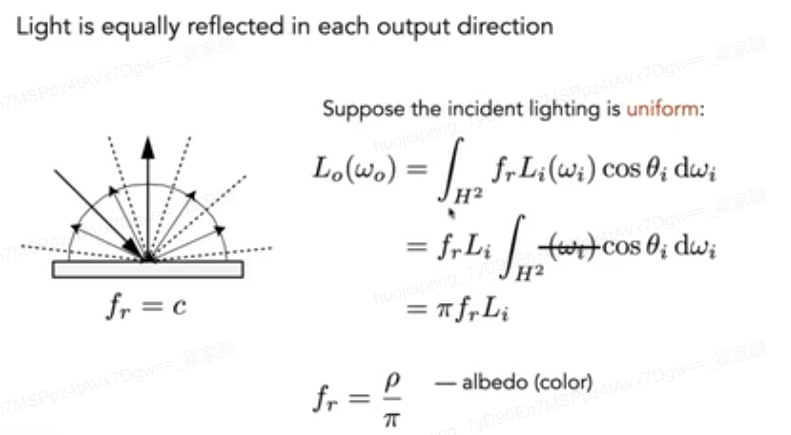
举例:镜面反射,一个光就会被反射到较集中的出射方向上,漫反射,一束光就会被均等地反射到各个方向上
-
反射方程
对于每一个入射方向dwi全部加起来,对于每一条光线,都可以通过BRDF计算出其特定出射角度的反射比例,用入射光的irradiance与此比例相乘并进行半球积分即可得到 反射方程
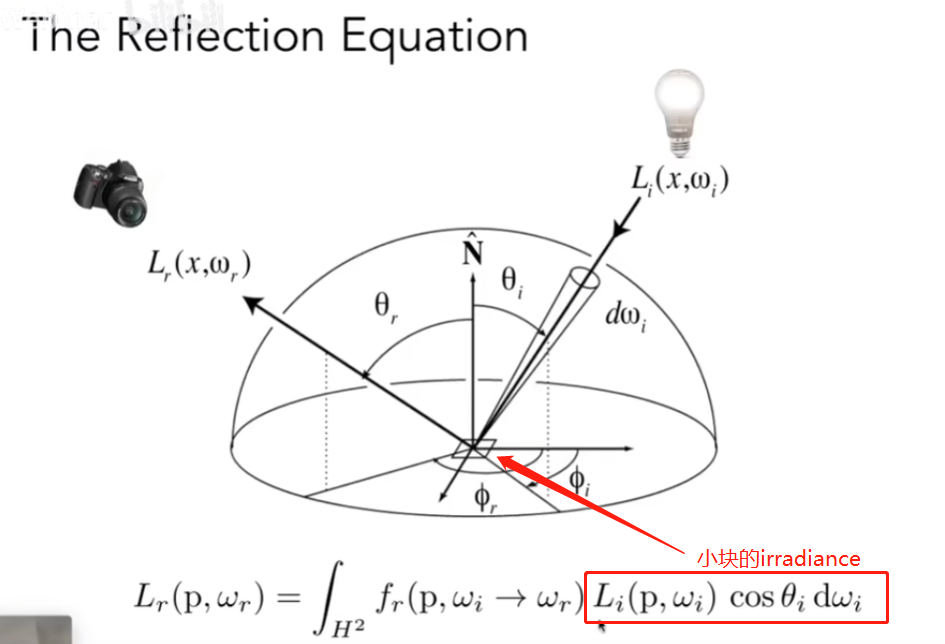
-
渲染方程
任何一个出射的radiance也有可以为其他面上的入射radiance,因此这里会出现递归的情况。
半球(表示做 或 +)
所有的限制在物体表面的渲染都满足以下的方程:

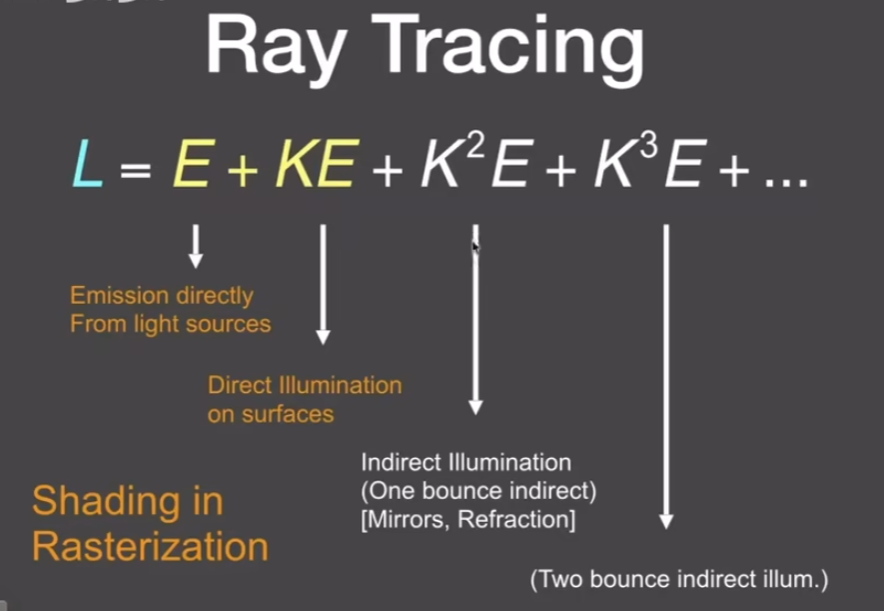
更完整的渲染方程

对渲染方程进行变换,在前两次,直接光照+一次间接光照可以通过光栅化来解决,但后面多次间接光照则需要用到光线追踪
蒙特卡洛积分
概率论相关
连续的情况: Probability Distribution Function.这样的曲线描述,某一个点x取旁边的dx的值,其中的面积就是概率密度p(x), pdf 概率密度函数:正值,积分一起为1
期望值 = 每个值与概率(连续的就是p(x))相乘,加一起求和/个数
蒙特卡洛:计算定积分,结果为一个数
在曲线a,b之间采样
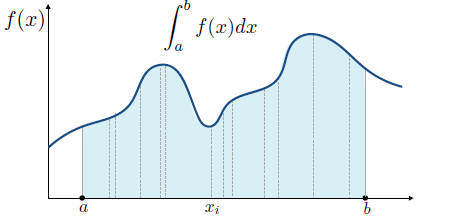
特点:
在积分域上以一定的PDF进行采样,对每个样本算f(x)/p(x),然后平均起来
- 定义在X上的积分,一定得采样X
- 需要知道f(x), p(x)

路径追踪 Path Tracying
whitted Style Ray Tracying的问题
- Glossy的物体的反射问题 — Utah 壶
- 全局光照的问题(Color Bleeding现象) — The Cornel Box
虽然Whitted Style是有问题的,但是渲染方程对的。因此需要正确的解出渲染方程。
渲染方程 = 自发光 + 其他光源,反射的radiance的积分 ? 使用蒙特卡洛的方法解
因此转换问题为,在半球面上采样,需要找出对应的f(x)和pdf函数p(x)


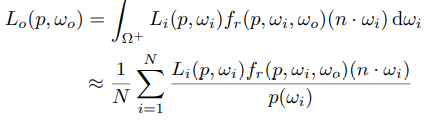

基本描述的方法的问题:
- 过多的光线递归? 指数级增长
- 递归的算法没有出口?
对于1:
只有N等于1 时候,是不会爆炸的
对于N=1时的蒙特卡洛积分的渲染方程解法,这种方式叫做Path Tracying
对于N不等于1,分布式光线追踪
但N为1,结果会过于Noisy,为了解决这个问题,使用Ray Generation, 生成多条path
如何处理noisy的结果?随机的从相机方法取点

对于2:
Russia 轮盘赌的方法决定是否退出
以一定的概率打光线,最后再把概率除掉(离散型随机变量)
解决完,得到最终正确的路径追踪解法

spp: samples per pixel 每个像素点的采样率
但是不高效,更加优化的方案:
光线的采样如何更加高效化呢? 理想的情况是反向以反射到的点去找光源
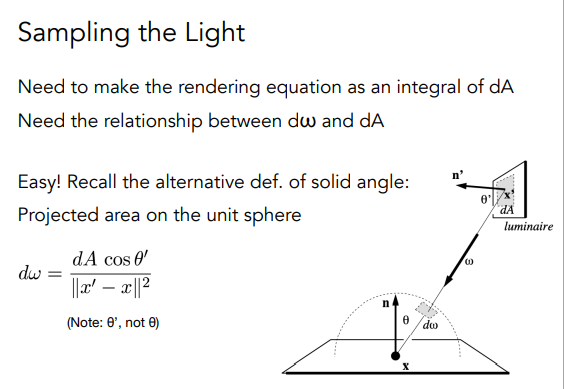
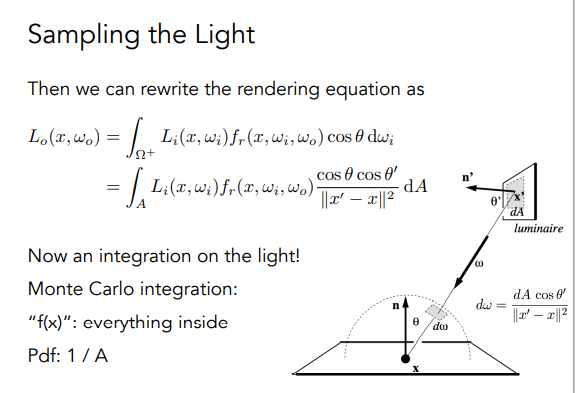
最终的优化版方案:

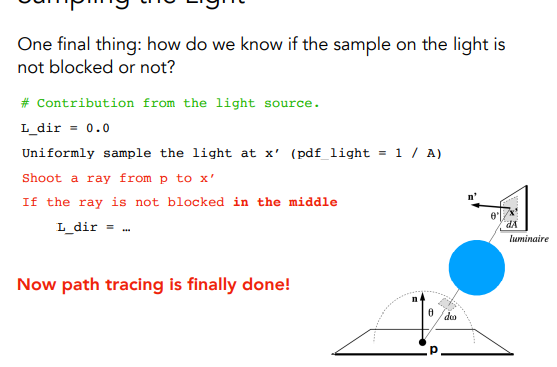
总结: Path Tracying 100%正确的效果,几乎完美的复刻现实