计算机图形学编程笔记1
图形学概论
- 特效是最简单的图形学应用
- 字体的原理,点阵与矢量
- 实时的定义:达到至少每秒30帧级别
- Qt: 读Q"t"发音
一、搭建OPENGL 的C++环境
- 1.1 准备工作
- VS下的C++环境
- 窗口显示库: GLFW
GLFW 安装编译的方法,32位使用编译会有问题,这里如果用64的话是: 具体细节
- 进入GLFW官方网站glfw.org,下载源码
- 安装CMAKE,使用CMAKE编译源码生成工程
3.生成完工程,打开工程,编译生成lib文件
3.扩展库: GLEW,官网下载 取出lib和dll文件即可
4.数学库:GLM, 官网下载完即可。
5.纹理库:SOIL2
SOIL2 安装方法:具体细节
- 下载SOIL2源码
2.下载premake4
3.将premake4放到SOIL2的文件夹
4.终端cd到SOIL2的文件夹,执行命令: premake4 vs2012, 将生成工程文件
5.打开上面生成的VS工程,编译即可得到库
-
1.2 制作项目模板
1.准备lib文件夹,放glew,glfw, soil2的lib文件
2.准备include文件夹,放GLEW的GL文件夹,GLFW的GLFW文件夹,glm文件夹, SOIL2的SOIL2文件夹。
3.新建VS空C++项目,配置为win32
4.配置项目的VC++的常规里的包含目录,添加Include文件夹
5.链接器配置,常规添加lib文件夹,输入配置前面三个lib文件名加上opengl32.lib -
1.3 正式的项目开发
- 使用1.2创建的模板新建工程
- 拷贝glew32.dll到项目的debug或release目录中。
二、3D图形数据
2.1 绘制流程描述:
- init() 初始化时
-
- 创建一个缓冲区
-
- 将顶点数据复制到缓冲区
- display()每帧刷新时。
-
- 启用缓冲区
-
- 将缓冲区数据绑定至顶点属性
-
- 启用顶点
-
- 使用glDrawArray画出来。
2.2 VAO(Vertex Array Object), VBO(Vertex Buffer Object)
顶点数据会先放在一个缓冲区,而这个缓冲区就存储在VBO里。同场景可能有多个VBO。
顶点数组对象则是opengl3.0引入的类似于VAO的组织性结构。
例: 当绘制两个对象时,可以声明两个VBO,一个VAO,glGenVertexArray生成VAO,glBindVertexArray激活VAO与顶点属性关联,再使用glGenBuffers生成缓冲区。
2.3 使用统一变量
在shader中将变量标记为Uniform后,在opengl中使用glGetuniformlocation得到对应的GL 的id。这样再通过glm::value_ptr取出对应的数值指针设值!。
统一变量在每次从顶点缓存区拿值时都是不变的,可以理解为常量
2.4 绘制立方体
- 1.VAO,VBO初始化
- 2.从相机的位置获取视角矩阵,V_MATRIX。 使用glm:translate
- 3.从物体位置获取模型矩阵,M_MATRIX。 使用glm:translate
- 4.从窗口,获取到P_MATRIX透视矩阵.。 使用glm:perspective
- 5.将MV,P矩阵传到顶点shader里
矩阵变换从右往左变换,将transMatrix * rotMatrix。先旋转再变位置。
注意shader中的设值:
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
glEnableVertexAttribArray(0);
注意Opengl的glm与GLSL中矩阵的定义规则:
GLSL中的矩阵与GLM都是以列读取的!
//glm的定义矩阵,以下两个矩阵变量是相同的,且以1,2,3,4为列往后排 |
2.5 使用矩阵栈来处理分层模型
- 例 :行星系统的实现流程
-
- 初始栈,实例一个vMatrix视觉矩阵
-
- 实现太阳:复制一个到栈顶,生成太阳的MV矩阵,复制一个到栈顶,生成太阳的旋转。画太阳,然后POP出太阳的旋转。
-
- 当前栈顶的是太阳的MV矩阵。以此复制到栈顶,生成行星的MV矩阵,复制到栈顶,生成行星的旋转。画行星,然后POP出行得的旋转。
-
- 当前栈顶是行星的MV矩阵,以此复制到栈顶,生成月亮的MV矩阵,生成旋转,生成缩放。
- 5.前面四个步骤,此时栈,共有四个元素。从顶到底分别是,月亮,行星,太阳,视觉矩阵。依次弹出清空栈。
2.6 优化策略
- display帧刷新函数中不要定义或申请变量内存
- 背面剔除:
- 1.使用glEnable(GL_CULL_FACE) 激活此功能
- 2.使用glFrontFace(GL_CCW)设置逆时针为正向
- 3.使用glCullFace(GL_BACK)将背面剔除(默认)。 GL_FRONT 和GL_FRONT_AND_BACK
纹理贴图-使用SOIL2
3.1 使用纹理贴图
- 1.使用SOIL_LOAD_TEXTURE获取到texture ID
- 2.构建纹理坐标,以左下角为0,0为定,右上角为1,1。把纹理2D坐标点与3D模型坐标相映射。
- 3.在display中使用glActiveTexture激活,用glBindTexture(GL_TEXTURE_2D, “注:1中的texture ID”)
- 4.vertex shader 收到纹理坐标传至 fragment shader
- 5.fragmenet shader中使用sampler2d采样器,利用4中得到的坐标点取颜色值返回。
3.2 多级渐远纹理贴图 Mipmapping - 避免校正采样误差伪影
- 纹理中存储相同图像的连续一系列较低分辨率副本 。大小将比原图像大1/3
- 如何在OpenGL使用:
- 1.激活纹理。glBindTexture(GL_TEXTURE_2D, textureRef);
- 2.使用glTexParameteri的GL_TEXTURE_MIN_FILTER 指明,四个方法:
- GL_NEAREST_MIPMAP_NEAREST//取最近的纹素
- GL_LINEAR_MIPMAP_NEAREST//线性
- GL_NEAREST_MIPMAP_LINEAR//双线性
- GL_LINEAR_MIPMAP_LINEAR //三线性
3.3 各向异性过滤-AF
恢复MIPMAPPING丢失的细节,标准MipMapping使用正方形分辨率MIP纹理,而AF可以使用各种矩形分辨率来采样。
if (glewIsSupported("GL_EXT_texture_filter_anisotropic")) { |
3.4 环绕和平辅
- 当纹理坐标不是[0, 1]\的范围时,需要设置填充参数:
- GL_REPEAT, GL_MIRRORED_REPEAT(当奇数时坐标反转), GL_CLAMP_TO_EDGE(0,1以外强设成边界值), GL_CLAMP_TO_BORDER(0,1以外的设成颜色)
3.5 透视变形
考虑情形如:矩形棋盘结构的纹理填充,在X轴旋转时将导致三角面交接处发生变形。
默认opengl将会开启透视修复。
使用noperspective 禁止opengl透视修复
noperspective in texcoord;//片面
三、数学
1.1 点乘
Dot Product
向量点乘规则:
对应坐标的相乘的和: (x1,y1) Dot (x2,y2) = x1x2 + y1y2
向量点乘的几何应用:
- 查找两个向量之间的夹角
- 找一个向量到另一个向量的projection
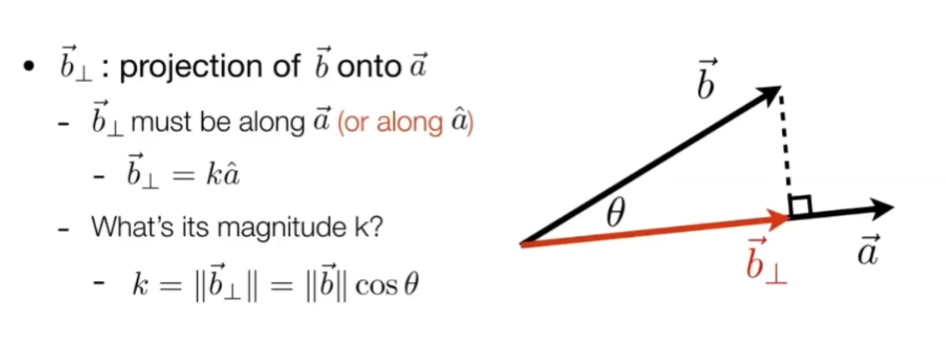
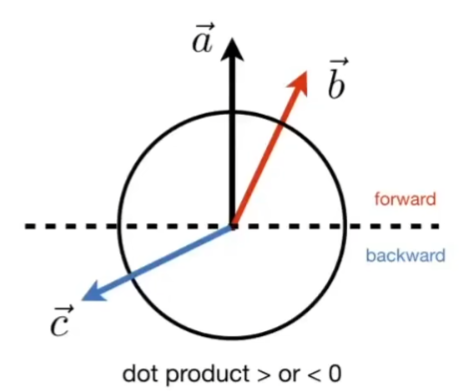
3.计算两个向量有多接近
4.关于一个前与后的信息
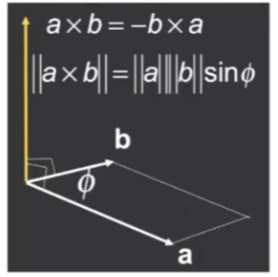
2.2 叉积
Cross Product
叉乘会垂直于初始两个向量
方向取决于右手螺旋定则
当x cross y = +z时,称为右手坐标系
(unity使用左手坐标系)
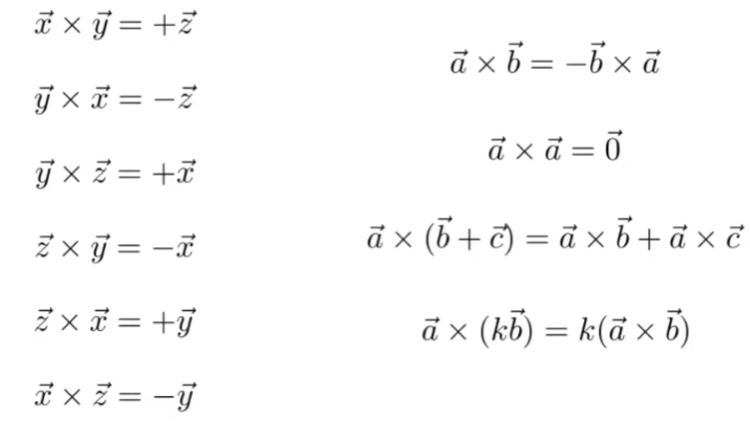

作用:
-
判定左右
当a cross b = +z时,a在右
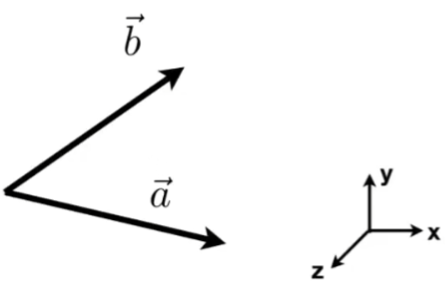
-
判写inside/outside
AB cross AP = +z 同时 BC cross BP == +z 同时 CA cross CP == +z 这时在inside 否则必为outside
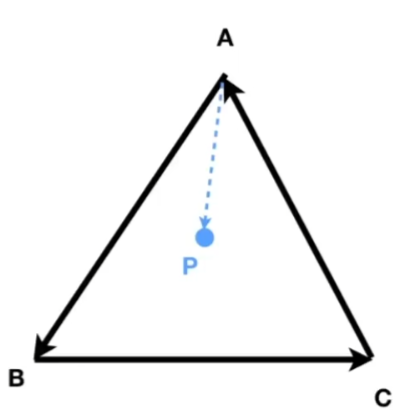
-
以任意三个相互垂直的向量创建坐标系

2.3 矩阵
相乘,第一个矩阵的对应行的元素,与第二个矩阵的对应列的元素,两两相乘得到结果
由此可知,对于想得一个任意行列的一个结果的矩阵值,只需要取第一个矩阵对应行的向量,与第二个矩阵对应列的向量做点积即可!!
属性:
矩阵不支持交互律,但有结合律,A(BC) = (AB)C
转置矩阵:
行和列互换

单位矩阵:
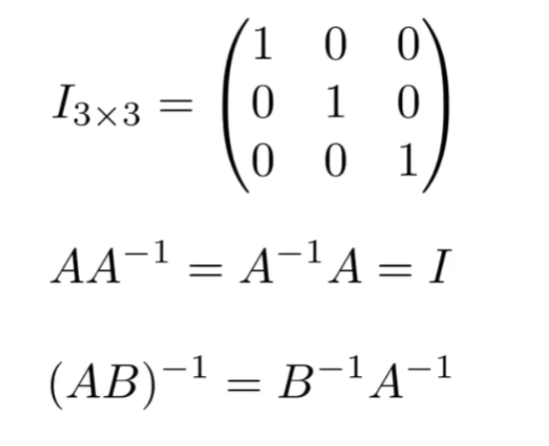
当两个矩阵相乘结果为单位矩阵,且不管顺序,则意为互为逆矩阵
矩阵在向量点乘的意义:
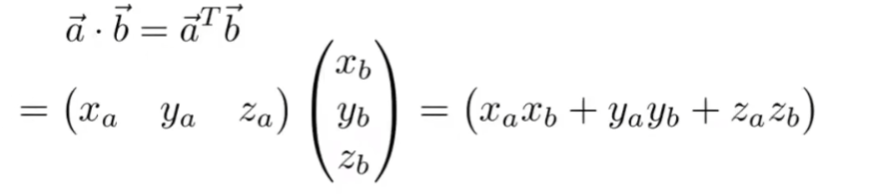
矩阵在向量叉乘的意义:

四、线性变换
共通性:线性变换:
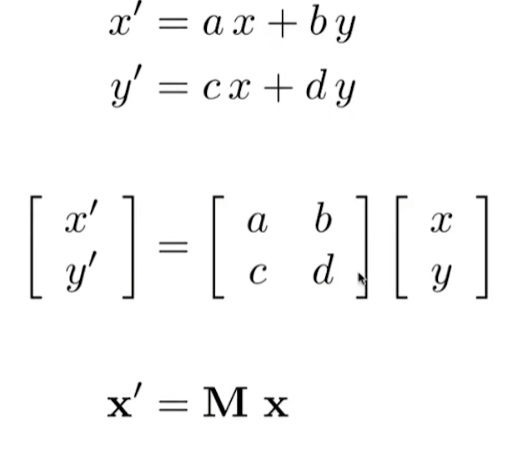
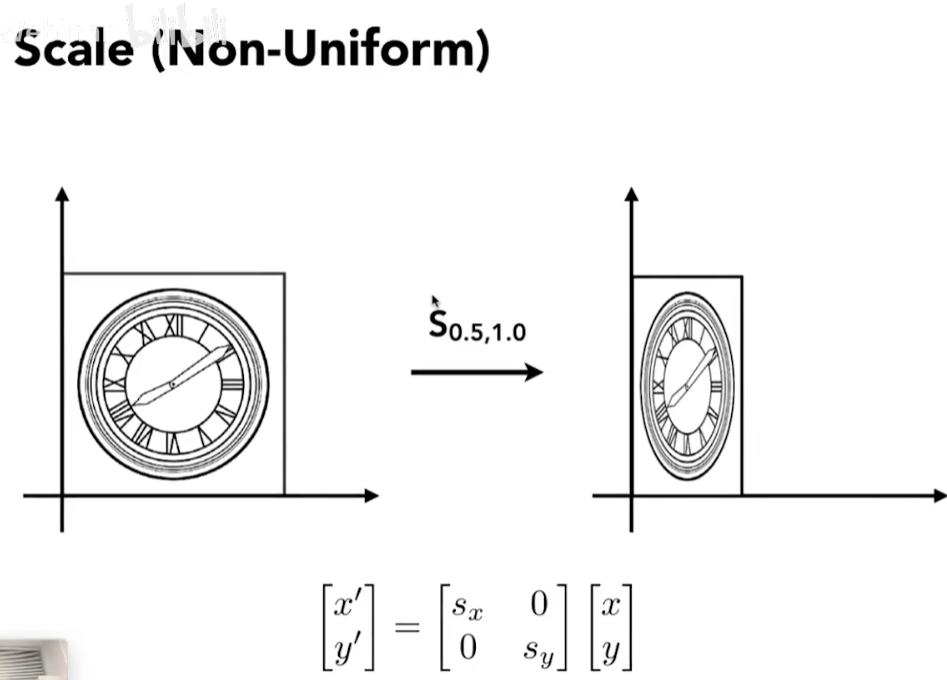
缩放 (’ 读为prime)
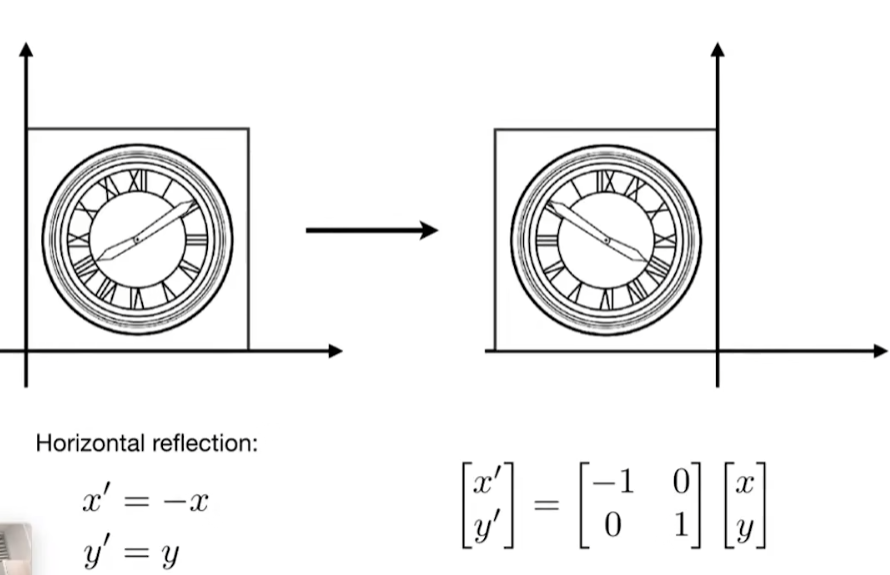
翻转
扭曲
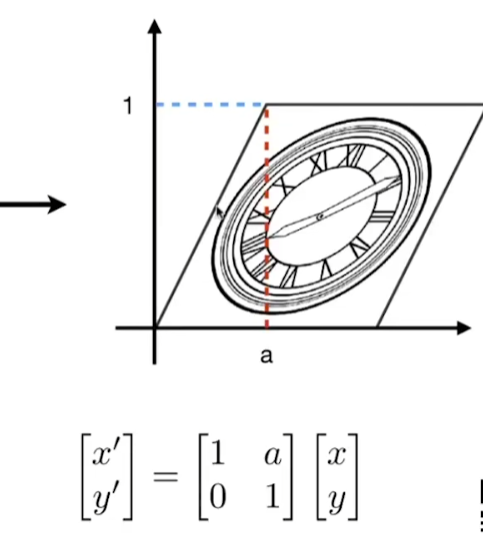
旋转
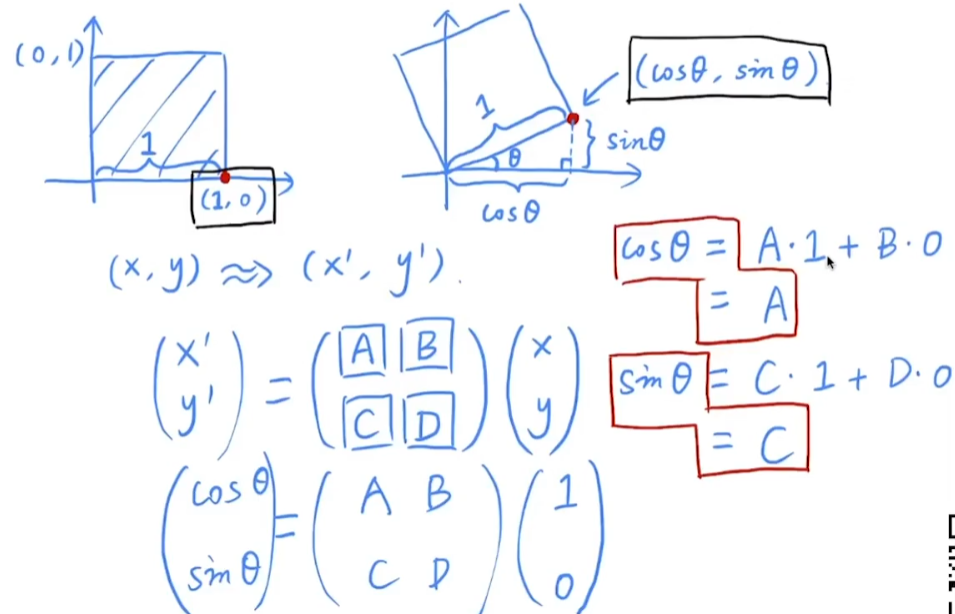
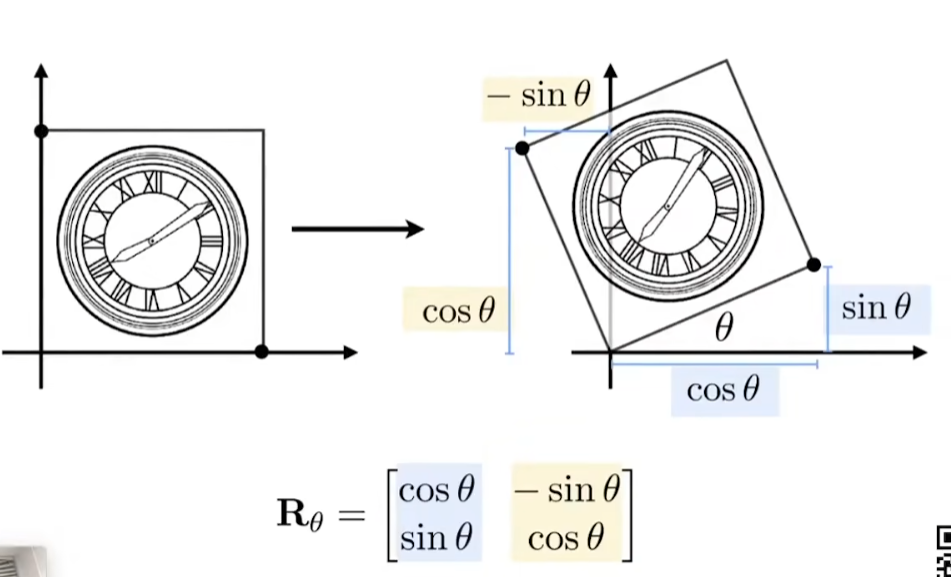
五、Homogeneous Coordinate 齐次坐标
- 问题:平移的变换并不是线性变换(即不可以写为 x’= Mx)
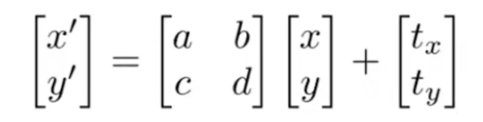
齐次坐标中引入了w坐标值
有没一种矩阵可以统一表示各种各样的变换?
为了使用线性变换的方程来表示带平移的变换,这时齐次坐标就发挥了作用:
- 对于 向量,齐次坐标w值为0 (x, y, 0), (x, y, z, 0)
- 对于 点, 齐次坐标w值为1 (x, y, 1), (x, y, z, 1)
对于两个点相加的齐次坐标的意义,其实是求两个点的中点

仿射变换:

齐次坐标:
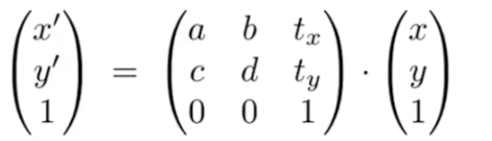
齐次坐标下的二维点变换:

特征:
当x’ = Mx 成立时, x = M-1x’也成立。 即如果需要还原,则使用变换矩阵的逆矩阵变换即可
六、组合变换
无论二维还是三维,都是先线性变换,再平移
矩阵的组合相乘是从右往左算

- 启示:由于矩阵有结合律,可以对于复杂的变换,把变换的矩阵先乘在一起,如常用的MVP矩阵
七、三维变换
平移变换和线性变换一起称为仿射变换
旋转的逆矩阵与旋转的转置矩阵是相同
数学上如果逆矩阵与转置矩阵相同,则为正交矩阵
y轴旋转矩阵不同的原因是, z cross x = +y,与x cross z的结果方向相反了
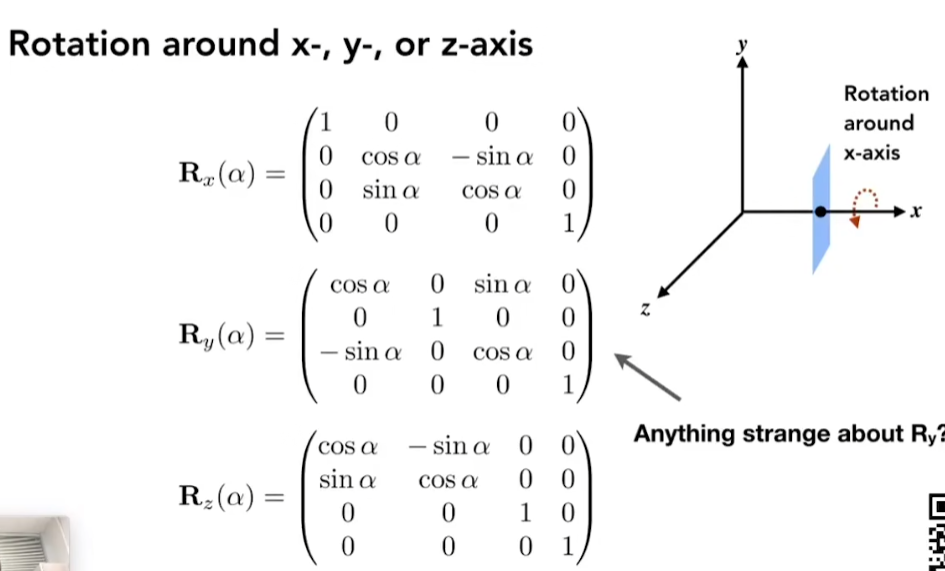
- 任意的旋转都能分解为三种旋转:
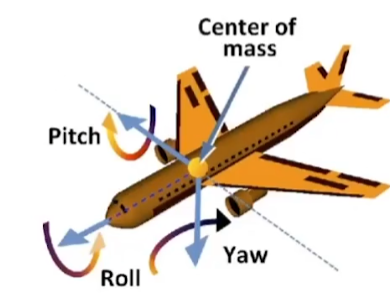
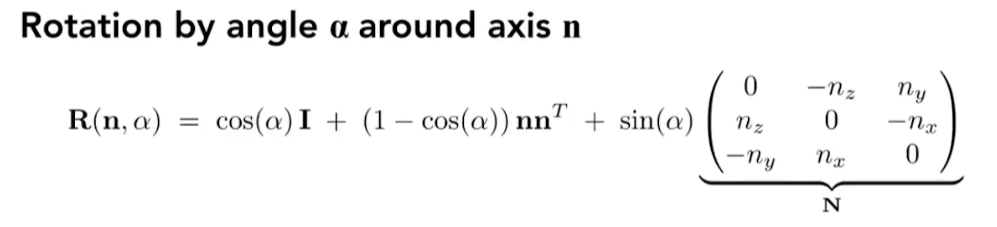
八、View变换/相机变换(Model-View Transformation)
将物体变到以相机为坐标系,即相机归成原点为轴
设定相机位置为e,看的方向为g,相机向上为t, 需要变以uvw构成的坐标系,设定w为-g的方向,u为t和w的叉积方向。
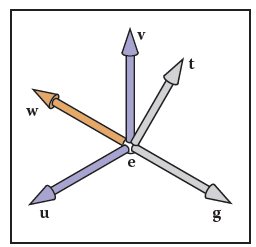
反向:假设已经得到uvw,变为XYZ如下:
由于旋转的逆矩阵与转置矩阵相同,即互为正交矩阵,因此,只需要得到此矩阵的逆即可
先进行平移变换, 再进行变换,:
九、Projection变换
- left plane,
- right plane,
- bottom plane,
- top plane,
- near plane,
- far plane.
正交变换
- 1.将所有模型所在的空间的中心点平移至原点。依据模型变换中的平移矩阵,其实就是平移空间中心坐标的负值
- 2.将空间的坐标轴数值缩放至 [-1, 1]³ 的标准立方体中。依据模型变换中的缩放矩阵
透视变换:
变换过程:透视投影的空间是一个四棱台,因为正交投影的矩阵已知,所以可以先将四棱台“挤压”为一个长方体,然后再对其进行正交投影。在“挤压”过程中,首先,近平面上的点坐标不变,因为最终就是投影到近平面; 其次,远平面上的点Z轴坐标不变,注意近平面和远平面之间的点Z轴坐标还是会变的,这也是产生“近大远小”的原因;最后,通过前两个性质,就限定了四棱台“挤压”为长方体只会有一种方式,即最终的变换矩阵是唯一的
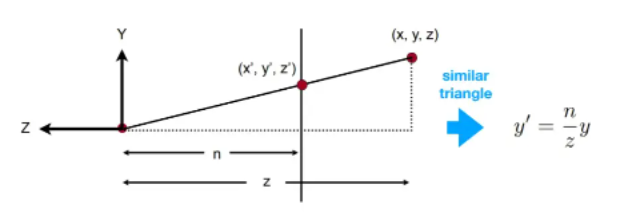
- 近平面的点的推导
对于近平面的点(x, y, n, 1) 经过透视变换,必定得到点(nx, ny, , n)
- 对于远平面的中心点的推导
对于远平面的中心点(x, y, f, 1) 经过透视变换,必定得到点(nx, ny, , f)
由上两种情况,得到如下“挤压”的变换方程:
因此,透视变换矩阵应为:先进行挤压,再进行一次正交变换
十、光栅化
The process of finding all the pixels in an image that are occupied by
a geometric primitive is called rasterization
一个完整的对象渲染可以划分为光栅化之前(几何过程), 光栅化,光栅化之后三个部分。
在进入光栅化后,数据应该为基于屏幕坐标的,光栅化后输出应该为各个面片,带有坐标信息及颜色信息
1. 相关概念
设t为高度,n为视线距离,FovY一般表示为垂直夹角,因此可以得到
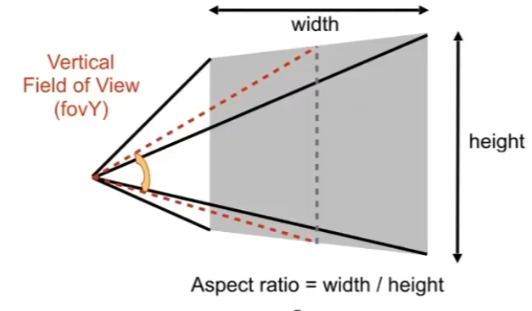
显示的最后一步,屏幕映射:
不考虑Z的情况下,将[-1,1] 坐标系转到[width,height]的视口坐标系
- 先平移到对应中心
- 进行比例缩放
光栅化:将图形(2维或3维空间)的进行打散成多边形显示到屏幕上的这个过程
这里的多边形在图形学中一般转为三角形,三角形优秀性质:
- 任意多边形都可以拆成三角形
- 三角形的三个点一定在一个面上
- 三角形内的一个点,更容易做差值运算,即都可以由其与三个顶点的关系得出差值渐变
2. 基础的实现
光栅化的重要过程:判断一个像素一个点与三角形的位置关系
- 一种简单的实现: 采样+inside函数
- inside函数的实现:使用点与三个顶点分别与各个边做叉积可以得到如果三个叉积都是正或者是负的,指定点是否在三角形内,是则返回1,否则返回0。
特别的对于在边上的点,根本不同的平台规定不同,如opengl则左上边算在三角形内。
- 由Inside函数,可以得出包围盒Axis Aligned Bounding Box(AABB):
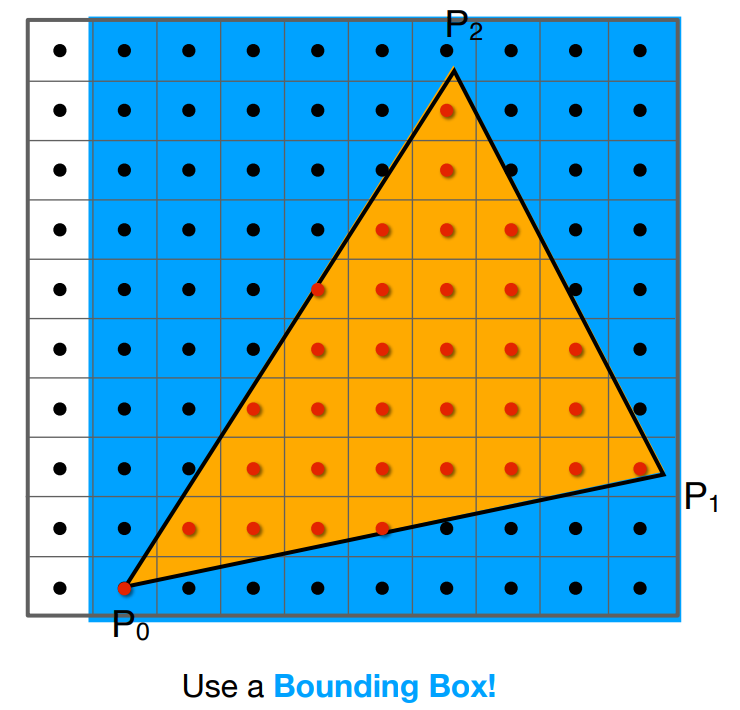
[Bayer Filter&Bayer Pattern]https://zh.m.wikipedia.org/zh-cn/拜爾濾色鏡
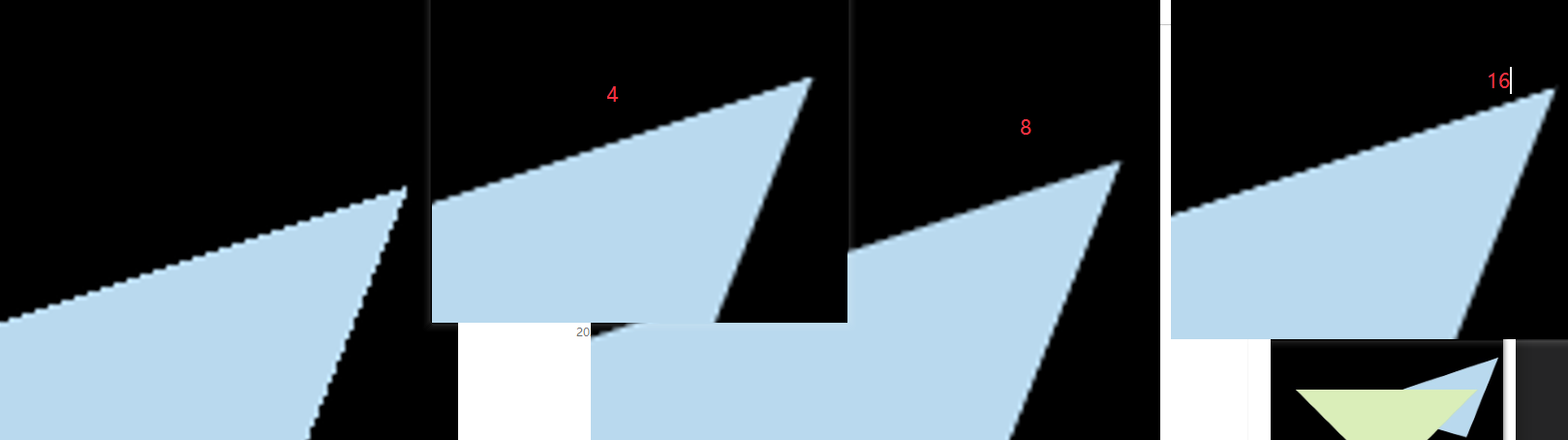
锯齿的形成,由于采样率的不足导致。
3. 抗锯齿和深度测试 Antialiasing and Z-Buffer
信号变化太快,导致采样跟不上,造成Artifact(走样、锯齿或Aliasing)
傅里叶积数展开:
任何一个周期函数,都可以写为一个正弦和余弦的函数组合
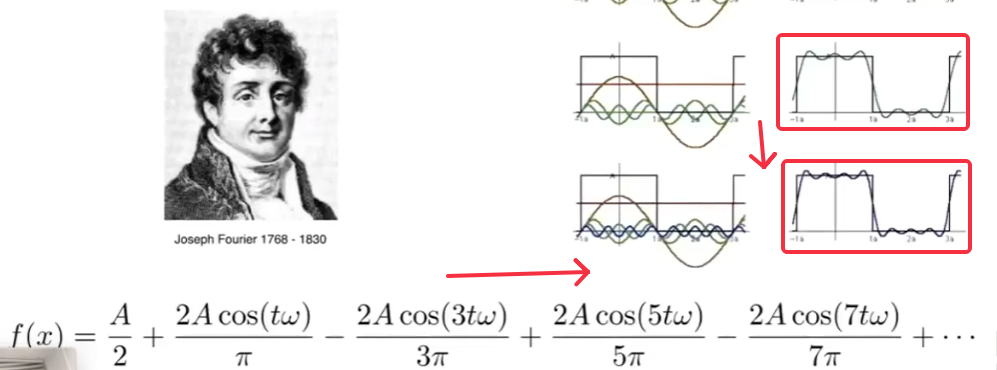
Antialias: 同样的采样方法去采完全不同频率的函数,得出结果却是相同的,无法区分!
滤波Filtering: Get ridding of certain frequency contents 删除某一频段的内容
关于卷积,频域,时域:
卷积:本质上是一种积分运算,公式也可以理解成先将一个函数翻转,然后进行滑动叠加。
卷积满足结合律,交换律,对于多个filter非常小的情况,较为实用的可以将多个filter先行做卷积运算
离散的归一化的filter: d[i] = …, 0, 0, 1, 0, 0,… 任意的一个信号与此做卷积的结果都会返回自己
如果我们把一个信号各个频段的成分也画出来,横坐标是频段的『大小』,纵坐标是对应频段成分的『幅度』,这样一个坐标系,我们把它叫做『频域』。把信号从『时域』映射到『频域』的手段,就是大家耳熟能详的『傅里叶变换』。
卷积的理解
以信号分析为例,我给出的输入信号是f从t=0才开始有的,而系统响应函数g也是从t=0开始的。在计算t=T时刻的卷积时,对g做翻转平移T,正好在0到T之间有重叠,其物理意义上面已经谈过,就是累积了时刻T以前发生的从0到T的所有输入效应,即从t=0开始的一段过去时间内发生的事情的效果。可是,在t>T时,对应的是未来的情况,在我们的函数中,由于这时候正好g=0,所以就不用考虑了。同样,t<0对应的是比时刻点为0的时候更早的事情,这时候f=0,就是说还没有输入进来,所以也不用考虑了。
对以上场景如果推而广之到无穷的情况, 那么计算时刻T的卷积,还需要考虑t>T的效果,即未来预期要发生的所有输入产生的效果,同时要考虑t<0的效果,即过去无穷大的时间内的输入产生的效果。这种情况从数学上理解是毫无问题的,但是要从物理上去解释,就比较的令人费解。但恰恰是这个情况,才完整了反应了卷积的“全局”的概念。
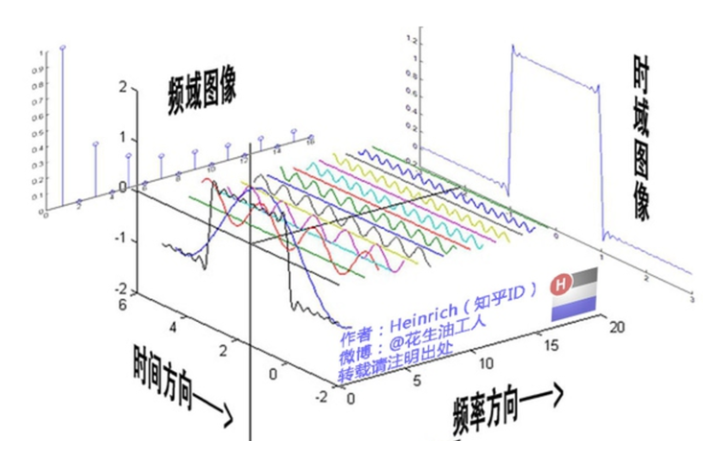
时域的卷积等于频域的乘积, 这种频域相乘的特性可以用于快速求一些特定函数的积分,因为『卷积』的本质是积分,而很多特定函数存在傅里叶变换和反变换,所以与其直接求解积分函数,不如把他们变换到频域,直接进行频谱函数『相乘』,然后再反变换回来,就得到积分结果了
采样:重复原始频谱。
产生走样的原因:频谱在采样重复过程中产生了重叠的现象
反走样的方法:
1.提高采样率(最直接的方式)
2.先做一个低通滤波,即做一次模糊,先去掉高频信号,再做采样
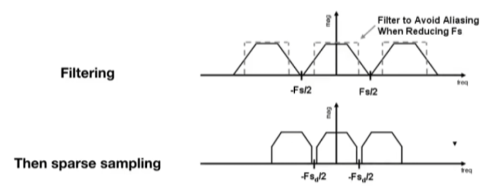
针对第二种反走样的一种方案:
MSAA(Multi-Sample Antialiasing):
解决信号模糊的解决文案:
- 对于任意一个像素点进行拆分更细的像素点
- 得到更明确的覆盖率
仅是为了得到更好的覆盖率,以得到模糊
Antialiasing的另外的方案:
FXAA(Fast Approximate), 得到有锯齿的图,找到边界锯齿更换为无锯齿的图。
TAA(Temporal) ,复用上一次采样的结果,复用时间维度上的结果。
思考:为什么先采样再模糊就不行? 提示,先采样则频谱已经混乱了,再模糊就不行了
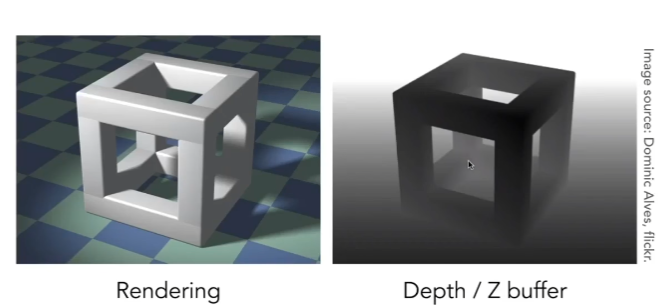
如何解决深度远近的问题:
算法:Z-Buffer
1.为每个像素记录最小的z值,离相机最近的距离
2.将1的数据的颜色信息记录到frame buffer中,z-buffer存储深度信息
实现明细:
- 光珊化过程中,假定所有的像素离相机最远
- 每次遍历如果任意一个像素比较近,则记录下来
十一、着色
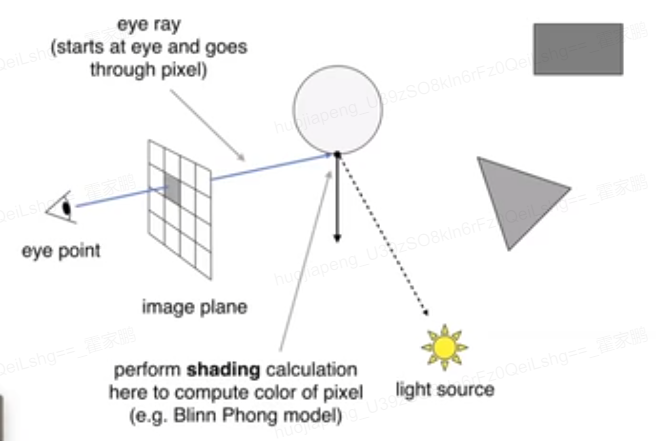
最基础的反射模型: Blinn-Phong
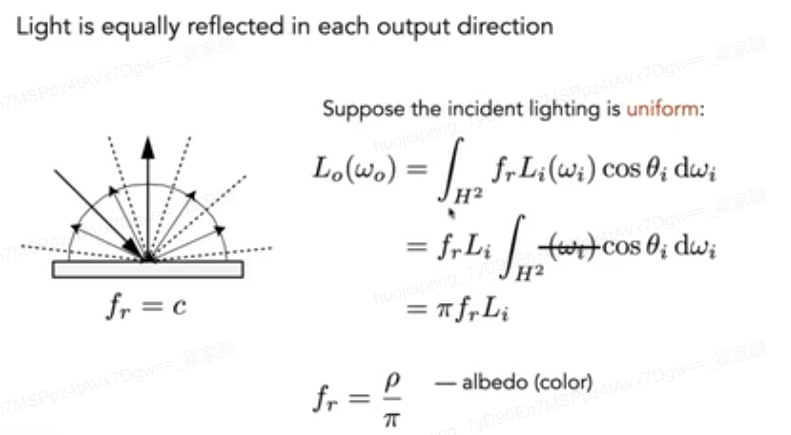
- Diffuse: Light is scattered uniformly in all directions. 漫反射将光源反射到各个方向
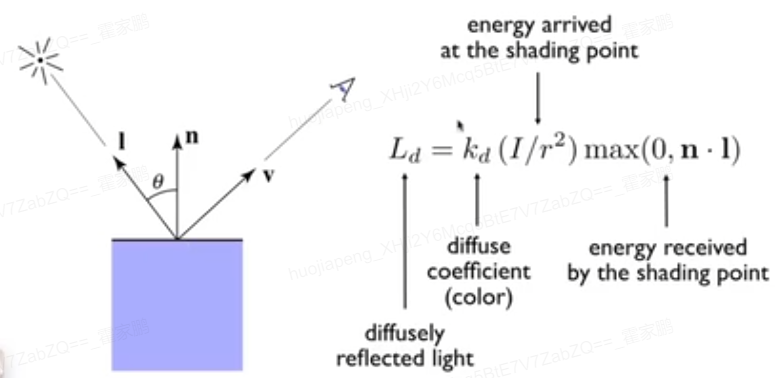
- Specular: 对于高光,观察的方向与镜面的反射方向接近时,得到高光
这种特性也可以归为l,v的半角方向与法线方向接近(即n和h足够接近)。 n和h的接近程度也可以表示v与r的接近程度,这样做的目的是减少reflect的计算,加快速度
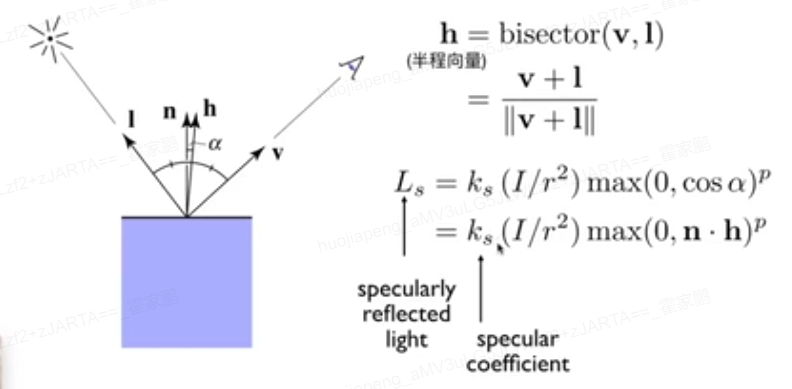
Phong模型,这里使用的是v与r(反射方向)的接近
Reflect推导流程: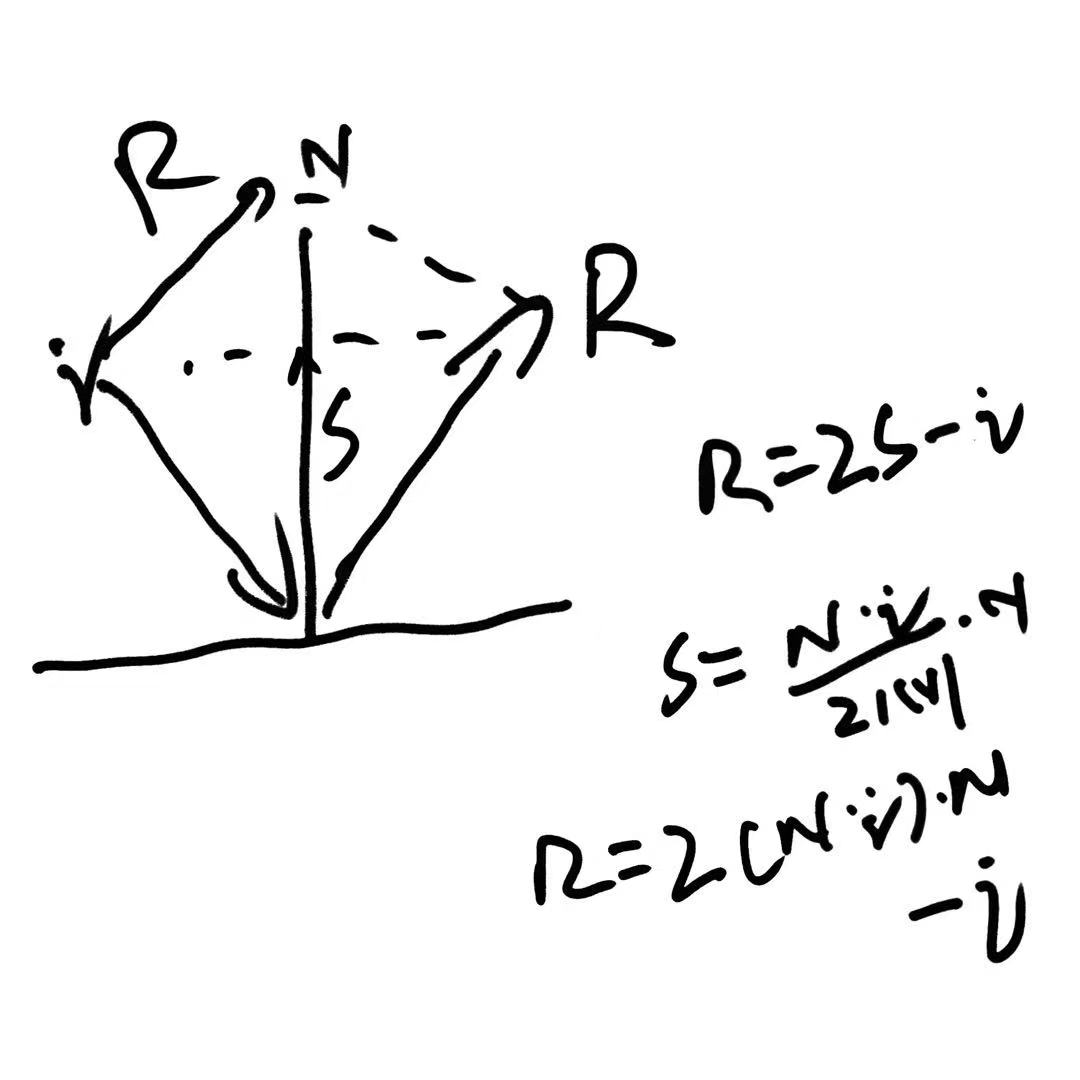
按指数将高光收到更小的一个点,一般这个值是在64-200左右,大概在3度左右的高光范围
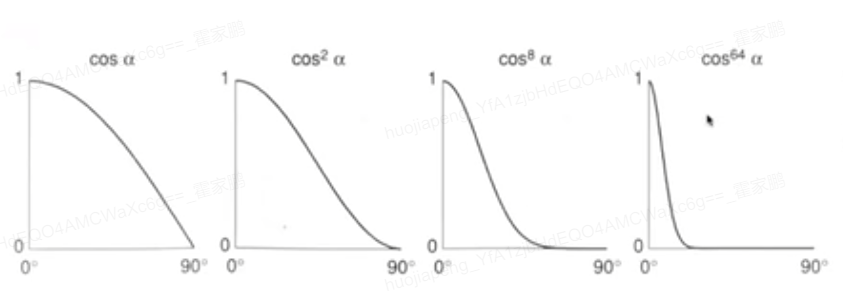
- Ambient: 环境光
La = KaIa
Ka : ambient coefficient
环境光可以考虑成一个常数,精确的计算需要全局光照相关的知识
Ambient + Diffuse + Specular = Blinn-Phong Reflection
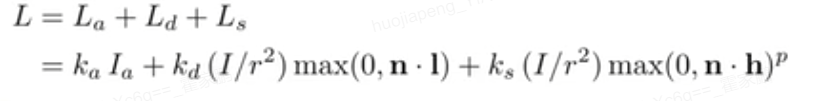
着色频率
- 逐面片 Flat Shading
- 逐顶点 Gouraud Shading
- 逐像素 Phong Shading
取决于面,顶点,像素出现的频率来选择哪种方式渲染

Q: 如何求逐顶点的法线:
以四周的三角面的法线,取其平均,再配以权重值,得出近似的顶点法线
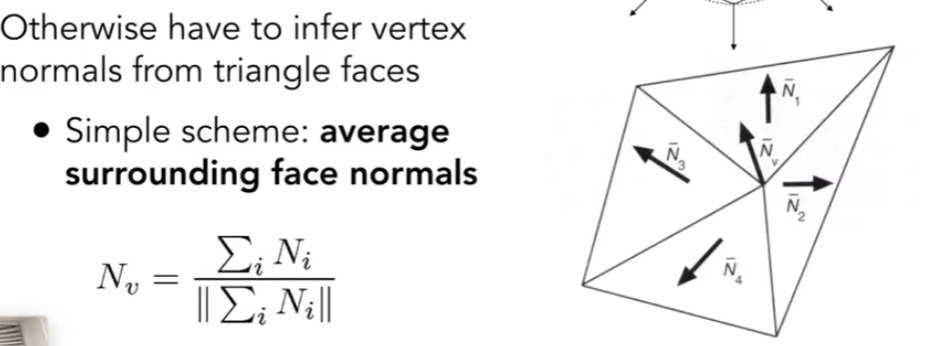
Q: 如何定义逐像素的法线(得到一个平滑过渡的法线?
两点之间的法线,取其重心坐标(Barycentric Coordinates),归一化之后得到过渡的法线
图形管线(实时渲染管线)
简言之,从场景到最后的一张图的过程
开始:Application
Vertex Processing
Triangle Processing
Rasterization
Fragment Processing
Framebuffer Operations
结束: Display
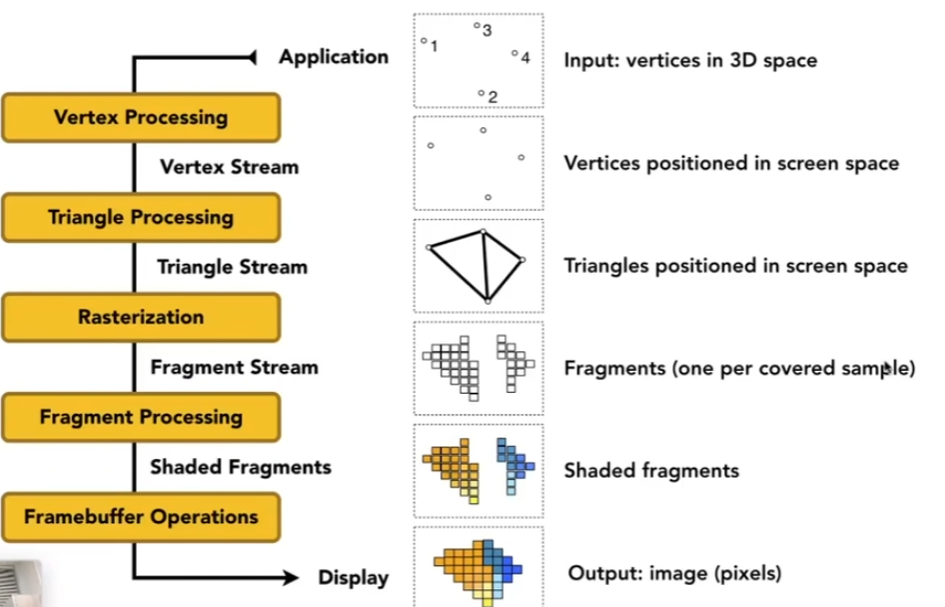
Shading可以在Vertex Processing也可以在Fragment Processing,而控制这里shading的过程称为Shader!
Shader不需要写For循环,只需要关于每个顶点和每个面片
使用Compute Shader可以实现更多的GPU计算,GPGPU(通用GPU)
纹理映射
任意一张图映射到一个物体的表面的过程
纹理坐标系: U横轴,V竖轴,范围是(0~1)
tiled纹理:无逢衔接纹理来不失原来效果
重心坐标 Barycentric Coordinate
如何在三角形内部做插值: Interpolation across Triangles
为什么需要插值:
- 特殊顶点
- 在三角形之间平滑过度不同的值
哪些需要插值:
Texture Coordinates, colors, normal vectors.
实现插值: 重心坐标
给定一个三角形所在平面上的点x,y。 有三个系数之和为1,且与三个顶点ABC线性组合
注意三个值都不可为负数
举例: A点的重点坐标
几何视角看,重点坐标也可以表示为面积比例:
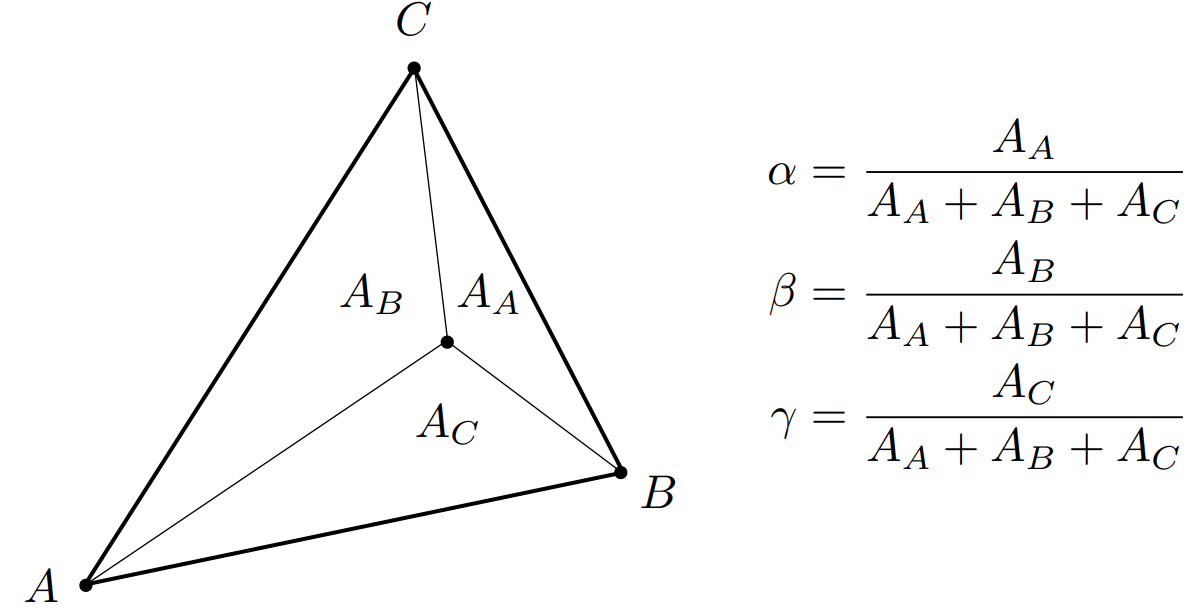
特别地,中心点的重心坐标:
重心坐标公式
投影变换下不能保证重心坐标不变!
由此,对于如三维坐标系的物体,在投影之后做插值求重心坐标是不一定对的,需要在原三维坐标中求
应用纹理
- 纹理放大问题
纹理元素texel, 一个像素在一个纹理
第一个可能的异常: 纹理图片过小?
- 双向插值: Bilinear Interpolation
找到指定点最近的四个点u01, u11, u00, u10,则插值就为
Two helper lerps
Final vertical lerp, to get result:
- 更好的效果-双三次插值:Bycubic Interpolation
取周围16个
第二个可能的异常: 纹理图片过大?
远处出现Morie, 近处出现Jaggies。
可能的方案: MSAA 加多采样点,可行但消耗过高
如果高效的拿到平均值呢? 对于任意不同大小的区域来做不同的范围查询
MipMap的方案:
MipMap: 从一张图生成一系列图,又叫图像金字塔
三个限制(fast, approx, square正方形的查询)的范围查询
在MipMap第D层去查找:
-
首先找到物体像素点附近一个像素的点,分别对应到纹理UV上
-
在纹理UV上算出近似的这个L边长
-
由L边长,可以得到应该采用哪一层的MipMap
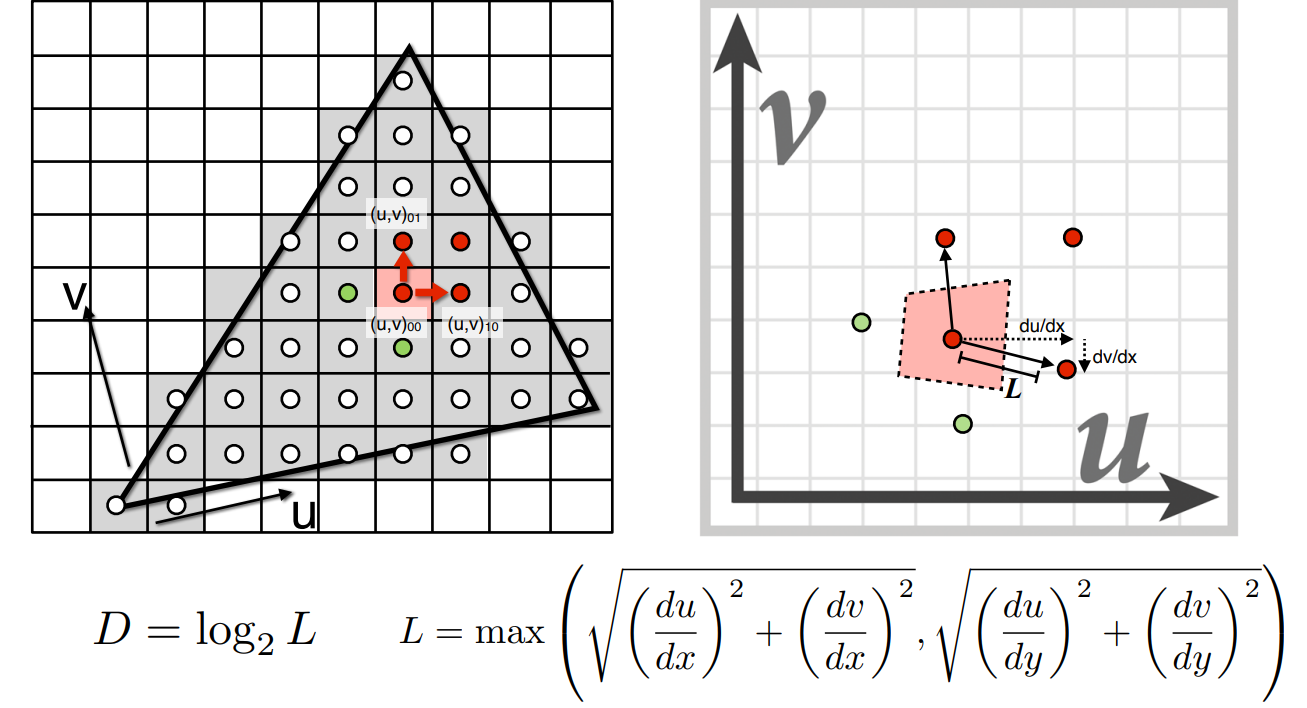
-
三线性插值
第三次插值, Trilinear Interpolation
为了MipMap层之间过渡问题,对层与层之间进行差值
三线性插值的问题,远处会overblur的问题。引入各向异性
效率消耗为4/3,即比原本的多1/3的消耗
- 各向异性过滤- Anisotropic Filtering
对比三线性插值,支持处理矩形的处理,对于MipMap的正方形的过滤,得到更好的效果,但并非完美。
还有可能处理非矩形非正方形的范围,则可以选择如EWA-过滤,其支持多重查询,权重值,支持处理不规则footprints
消耗为3倍
EWA-过滤,其支持多重查询,权重值,支持处理不规则footprints
- 环境贴图 Environment Map
用纹理描述一个环境光
各种经典模型
假设:环境光来自无限远处,只记住方向信息,没有深度的意义。
Spherical Environment Map: 把环境光记录在球上
为了解决球面的扭曲的问题,引出了Cube Map:
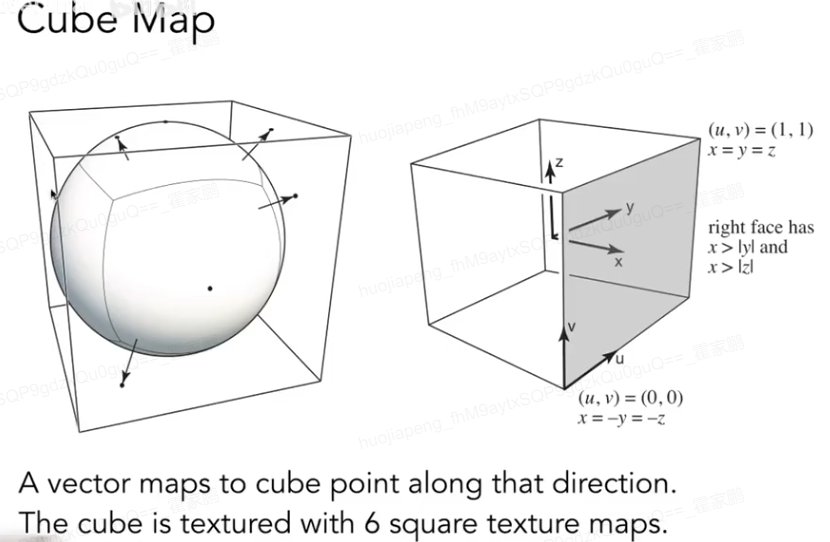
- 凹凸贴图 Bump Map
用纹理描述表面的相对高度差,又称为法线贴图。
用处:可以使用法线贴图实现假法线,伪装物体表面的情况
对每一个像素的法线进行扰动
复用贴图信息去改变每个像素的高度差
如何去影响法线:
以二维空间为例, 先取任一个点的切线,利用导数(水平方向移动一个距离)。再将切线逆时针旋转90(x,y互换)。
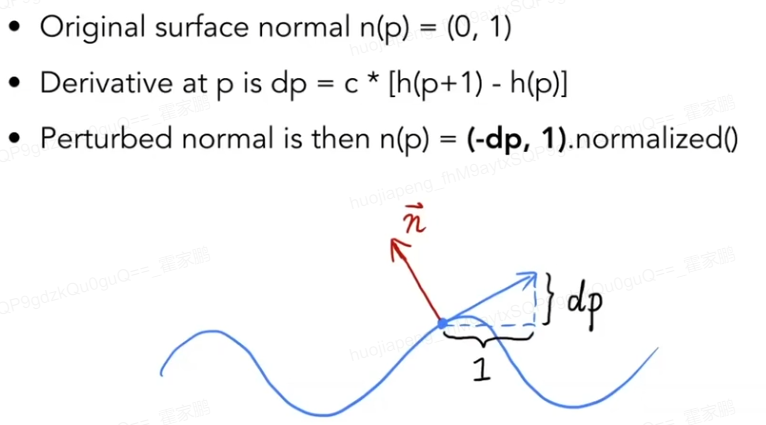
三维空间下,最后一步的推导过程省去得到添加负号的结果

特别的:
位移贴图 Displacement mapping, 也使用Bump Map的贴图,但对几何发生变更,实质上对顶点做一个位置移动
这种方式对模型面数有较高的要求,这样才能达到更好的效果。
扩展: DirectX 有一种动态模型细分面的技术
- Perlin noise 的三维噪声技术
- Ambient occlusion贴图
对于模型内部的阴影,可以使用纹理记录一些Ambient occlusion的信息。
几何
-
Implicit 隐式的几何
表示一定的关系,并不表示实际的点。更通用的公式: 若点满足 f(x,y,z) = 0,由表示这个点在几何的面上
特点:
判断一个面找什么样,有哪些点,很难。 HARD
判断一个点是否在不在几何内,小于0表示在内,大于0表达在外 =0则是在面上。 EASY -
Explicit显式的几何
将u,v的点可以显式的按公式映射到x,y,z。
特点:
通过uv找面上的点,会比较容易。EASY
判断在内外。 HARD
由此,几何并没有最好的表示方法,根据需要处理的问题,选择使用显式还是隐式。
在CG中,常用的隐式表示方法:
1. Algebraic Surfaces
代数的方法去描述表面
2. Constructive Solid Geometry
广泛应用在建模软件中
通过一些基本几何的基本运算来描述。
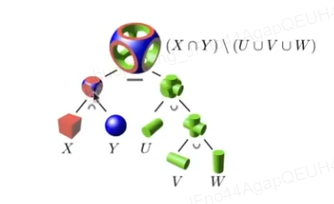
1. Distance Functions
定义一个距离函数(空间中任意一个点,到想到的一个点的距离)的方法的描述。
例子: SDF 有向的距离函数 Signed DF
求出各自的距离函数,最后找到f(x)=0的面
2. Level Set Methods
与DF相同,区别只是把等高线找出来,关注f(x)=0的面
3. Fractals 分形
拥有自相似的物体。
常用的显式表示方法:
1. Point Cloud
一个点的x,y,z的列表。通过一堆点堆积,需要非常多的点才能表示。通常会变成三角面,将点的密度太小时比较难以画出来
2. Ploygon Mesh
CG中最广泛应用
多边形面,更容易模拟和渲染,更复杂的数据结构
> obj文件中存储的点,法线,纹理,坐标分开表示,最后连接起来将结果放在后面。
> 如f 5/1/1 1/2/1 4/3/1 三个点,每个点的第一个参数表示哪个点,第二个参数表示uv坐标,第三个参数表示法线
曲线 Curves
应用:Camera path, Animation curve, Vector fonts
-
Bezier Curve:
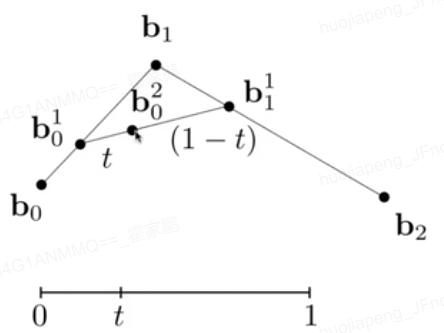

性质: Affine transformation 前后不变
凸包性质,找到最小凸多边形可以包含所有的点,生成的点一定在是选中的点形成的凸包内 -
Piecewise Bezier Curves 分段的BC
将一个大的BC,分成多个小段,对两个小段生成多个点,让生成的点再生成曲线。
参考网站 -
Splines 样条
满足连续性,有一系列的点连接。 一个可控的曲线。
B-splines: 对BC的扩展,包括所有BC的属性。局部性的特性: 改变一个点,明确改变的的范围
https://www.bilibili.com/video/av66548502?from=search&seid=65256805876131485
网络处理
细分 Subdivision
- 第一: 把三角形的数量增多
- 第二:调整三角形的位置
-
Loop(人名,非循环的意思) Subdivision:
对于新旧顶点,分别改变其位置。只能处理三角形面- 新顶点, 取权重值
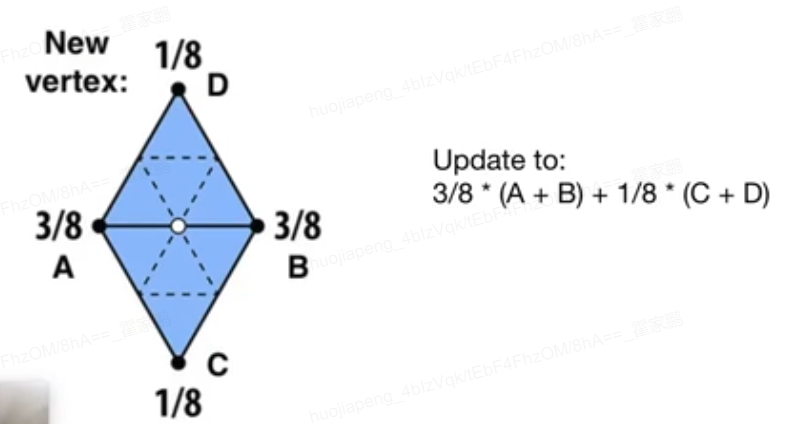
- 旧顶点,根据顶点的度(连接的边数)决定是否由周边的点决定(度越大,越应该由周边点决定)
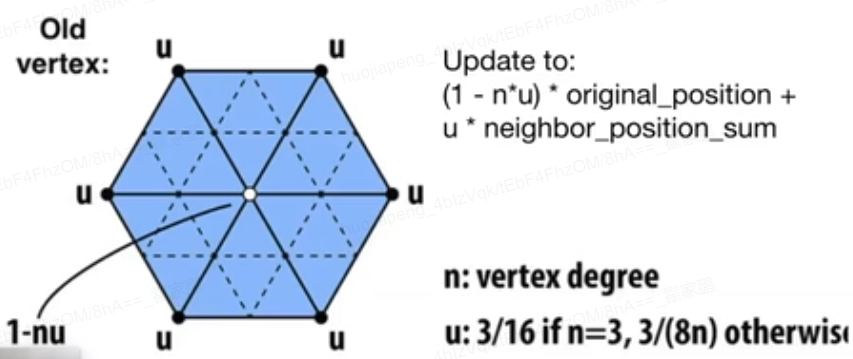
- 新顶点, 取权重值
-
Catmull-Clark Subdivision
概念:奇异点,度不为4的点
对于奇异点,做一次细分,对第一个边和每一个面,取一个平均的点,然后连接起来。 这时会产生新的奇异点,但会让所有非三角形的面消失。
重要的特性:
- 奇异点在做完一次新增后,再继续执行细分就不会产生新的奇异点了。
- 优点是可以用在各种面上,不仅仅是能处理三角形面

简化 Simplify
Collapse An Edge
坍缩一些边到更少的边
贪心算法,使用二次度量误差法找到点,坍缩边。 此点到任意一个点的平方和的距离最短
- 出现的问题,当找到一个点后,由于影响到了其他边,所以需要再更新一次。这里推荐使用的数据结构是:堆,优先队列
阴影
做两次光珊化深度图再比较深度图的信息
Shadow Mapping
同时被光看到,也被相机看到,这些点必定不在阴影里
Pass 1: 通过光源做一次光珊化,只取深度图 Shadow Map
Pass 2A: 由视角方向得到一张深度图
Pass 2B: 比较1, 2A的Shadow map。 如果一个点的光源得到的深度,与视角得到的深度不同,则这个点一定是在阴影。实际深度与光源的深度不一致,则点在阴影上
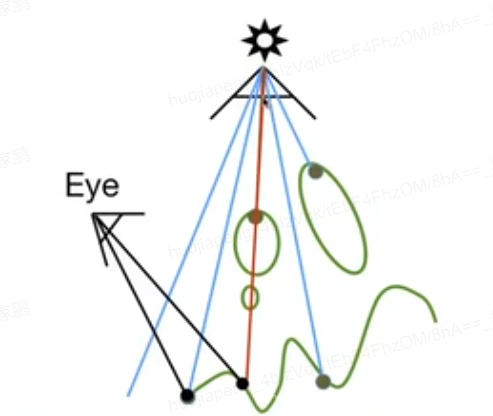

软阴影, 硬阴影。
本影区域:完全看不到光源,Umbra
部分看到光源,Penumbra
软阴影: Umbra Penumbra 及完全无阴影的过渡
有软阴影的前担一定是因此光源有一定的大小