贝塞尔曲线

转自： https://www.zhihu.com/question/29565629

贝塞尔曲线的历史:贝塞尔曲线于 1962 年，由法国工程师皮埃尔·贝济埃（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计,贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发，以稳定数值的方法求出贝塞尔曲线.
https://www.jasondavies.com/animated-bezier/

如果仔细观察这些曲线，你会立即注意到：

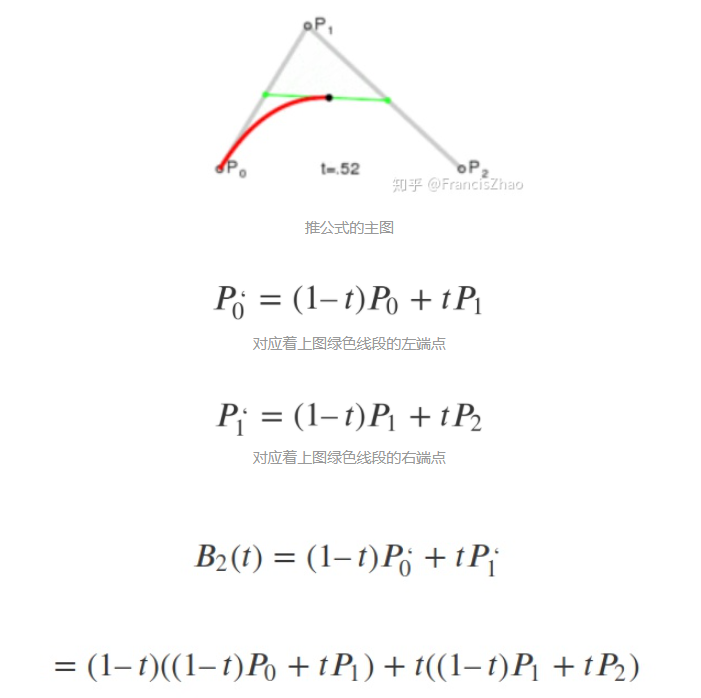
• 控制点不总是在曲线上这是非常正常的，稍后我们将看到曲线是如何构建的。
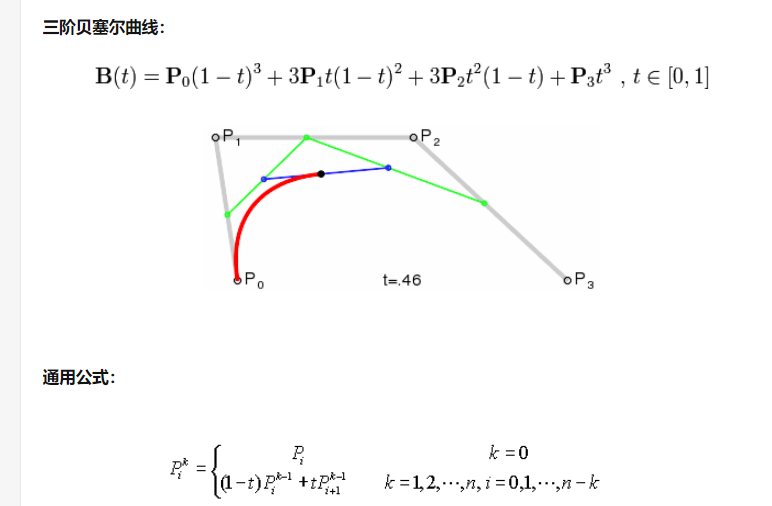
• 曲线的阶次等于控制点的数量减一。 对于两个点我们能得到一条线性曲线（直线），三个点 — 一条二阶曲线，四个点 — 一条三阶曲线。
• 曲线总是在控制点的凸包内部：

实现：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class BezierTest : MonoBehaviour
{
    public struct SplineData
    {
        public Vector3 P0;
        public Vector3 P1; 
    }
    public GameObject SampleObj;
    private List<GameObject> allObjs = new List<GameObject>();
    private List<Vector3> allPoss = new List<Vector3>();

    public LineRenderer lineRender;

    private int curPoints = 0;
    public int PointCount = 3;

    public int LinePointCount = 20;

    public bool Gen = false;

    private int temp;
    // Start is called before the first frame update
    void Start()
    {
        
    }

    // Update is called once per frame
    void Update()
    {
        if (PointCount != curPoints)
        {
            CreatePointObj();
            curPoints = PointCount;
            Gen = true;
        }

        if (CheckChangePos())
            Gen = true;
        
        if (!Gen)
            return;
        
        SetLineRender();
        Gen = false;
    }

    void CreatePointObj()
    {
        foreach (var obj in allObjs)
        {
            Destroy(obj);
        }
        
        allObjs.Clear();

        for (int i = 0; i < PointCount; i++)
        {
            GameObject go = GameObject.Instantiate(SampleObj);
            go.transform.position = new Vector3(i,i,i);
            go.transform.localScale = new Vector3(0.2f,0.2f,0.2f);
            allObjs.Add(go);
        }
        
        allPoss.Clear();
        foreach (var go in allObjs)
        {
            allPoss.Add(go.transform.position);
        }
    }

    public bool CheckChangePos()
    {
        bool isChanged = false;
        for (int i = 0; i < allObjs.Count; i++)
        {
            if (isChange(allObjs[i].transform.position, allPoss[i]))
            {
                temp = i;
                allPoss[i] = allObjs[i].transform.position;
                isChanged = true;
            }
        }

        return isChanged;
    }

    public bool isChange(Vector3 p1, Vector3 p2)
    {
        float absX = Mathf.Abs(p1.x - p2.x);
        float absY = Mathf.Abs(p1.y - p2.y);
        float absZ = Mathf.Abs(p1.z - p2.z);

        if (absX > 0.1f || absY > 0.1f || absZ > 0.1f)
            return true;

        return false;
    }
    


    public void SetLineRender()
    {
        
        
        List<Vector3> allVectors = new List<Vector3>();

        if (LinePointCount > 0)
        {
            float step = 1.0f / LinePointCount;
            for (int i = 0; i < LinePointCount+1; i++)
            {
                
                Vector3 bezierPos = GetAllPos(i* step, ConvertVectorToSplines(allPoss));
                allVectors.Add(bezierPos);
            }
        }

        lineRender.useWorldSpace = true;
        lineRender.positionCount = LinePointCount+1;
        lineRender.SetPositions(allVectors.ToArray());
    }
 
    public Vector3 GetAllPos(float t, List<SplineData> allData)
    {
        if (allData.Count == 1)
        {
            return GetBezierPos(t, allData[0].P0, allData[0].P1);
        }
        else
        {
            List<Vector3> nVector3s = new List<Vector3>();
            foreach (var spline in allData)
            {
                nVector3s.Add(GetBezierPos(t, spline.P0, spline.P1));
            }

            List<SplineData> genSplines = ConvertVectorToSplines(nVector3s);
            return GetAllPos(t, genSplines);
        }
    }
    
    

    public List<SplineData> ConvertVectorToSplines(List<Vector3> allVs)
    {
        List<SplineData> result  = new List<SplineData>();
        for (int i = 0; i < allVs.Count; i++)
        {
            int next = i + 1;
            if (next >= allVs.Count)
            {
                break;
            }
            result.Add(new SplineData(){
                P0 = allVs[i],
                P1 = allVs[next]
            });
        }

        return result;
    }
    
    public Vector3 GetBezierPos(float t, Vector3 p0, Vector3 p1)
    {
        return (1 - t) * p0 + t * p1;
    }
    
    public Vector3 GetBezierPos(float t, Vector3 p0, Vector3 p1, Vector3 p2)
    {
        return Mathf.Pow(1 - t, 2) * p0 + 2 * t * (1 - t) * p1 + Mathf.Pow(t, 2) * p2;
    }
}