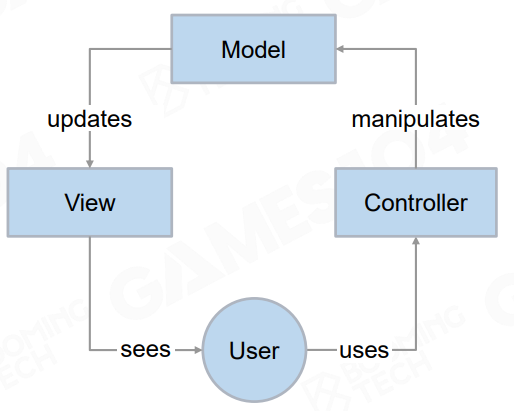
UnionFind
描述
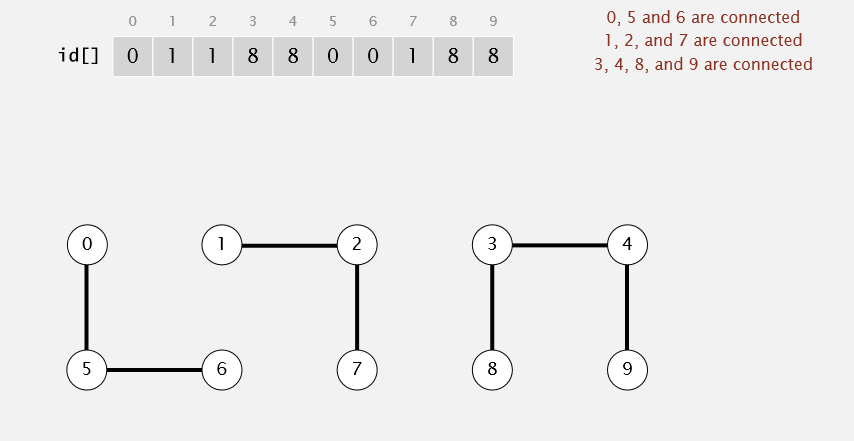
Dynamic Connectivity 动态连通性问题
假定的前提: p连q,则q也连p。
算法1: Quick Find -快速查找
数据结构
算法思路
分析
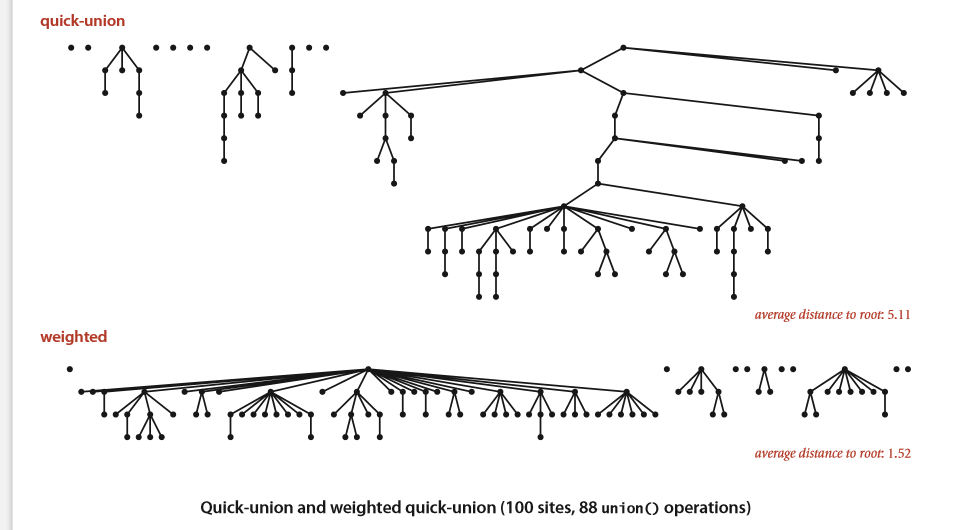
算法2: Quick Union -快速交集
算法优化一: 使用权重
实现:额外定义一个数组,存储树的权重,在添加时判定,只将权重小的往权重大的加
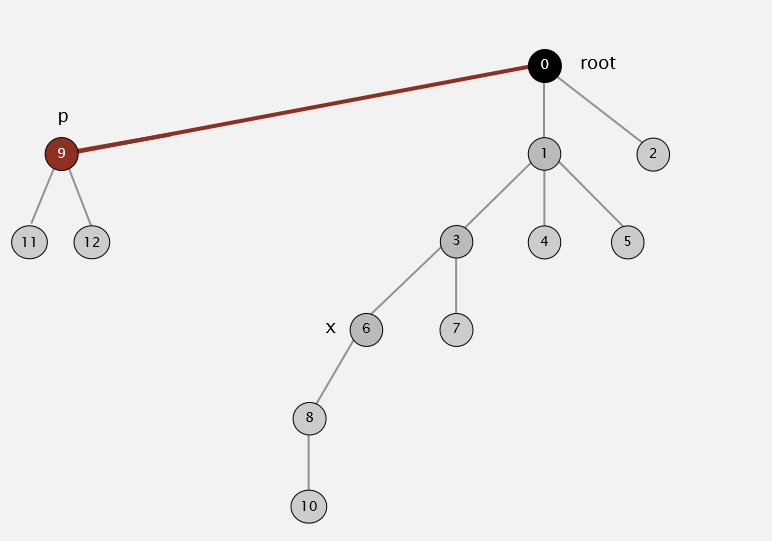
算法优化二: 压缩
Union函数调用时,对于多于一层的树,全部将真正的root改为当前的上级
C++实例、例子:
QuickFind_UF::QuickFind_UF (int N) { this ->length = N; this ->id = new int [N]; for (int i = 0 ; i < N; i++) { this ->id[i] = i; } } QuickFind_UF::~QuickFind_UF () { this ->length = 0 ; delete [] this ->id; } void QuickFind_UF::Union (int p, int q) int pid = this ->id[p]; int qid = this ->id[q]; for (int i = 0 ; i < this ->length; i++) { if (this ->id[i] == pid) this ->id[i] = qid; } Print (); } bool QuickFind_UF::Connected (int p, int q) return this ->id[p] == this ->id[q]; } QuickUnion_UF::QuickUnion_UF (int N) { this ->length = N; this ->id = new int [N]; this ->sz = new int [N]; for (int i = 0 ; i < N; i++) { this ->sz[i] = 1 ; this ->id[i] = i; } } QuickUnion_UF::~QuickUnion_UF () { delete [] this ->id; } void QuickUnion_UF::SetUseWeight (bool use) this ->useWeight = use; } void QuickUnion_UF::SetUseCompression (bool use) this ->useCompression = use; } int QuickUnion_UF::Root (int i) while (this ->id[i] != i) { if (this ->useCompression) { this ->id[i] = this ->id[this ->id[i]]; } i = this ->id[i]; } return i; } void QuickUnion_UF::Union (int p, int q) int pid = this ->Root (p); int qid = this ->Root (q); if (this ->useWeight) { if (pid == qid) return ; if (this ->sz[pid] < this ->sz[qid]) { this ->id[pid] = qid; this ->sz[qid] += this ->sz[pid]; } else { this ->id[qid] = pid; this ->sz[pid] += this ->sz[qid]; } } else { this ->id[pid] = this ->id[qid]; } } bool QuickUnion_UF::Connected (int p, int q) return this ->Root (p) == this ->Root (q); }
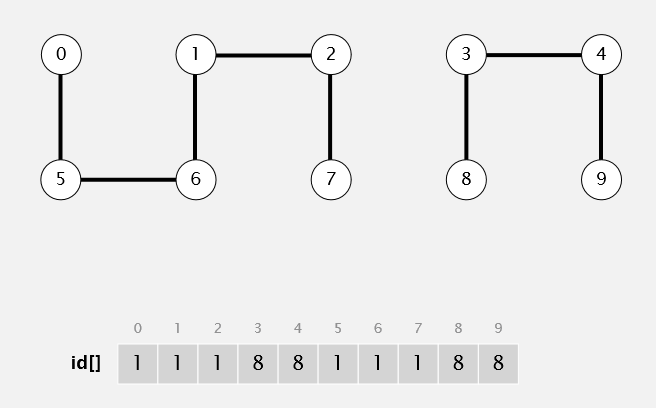
测试:数组为0-9,输入union: (4,3),(3,8),(6,5),(9,4),(2,1),(8,9),(5,0),(7,2), (6,1)
Quick Find 结果:
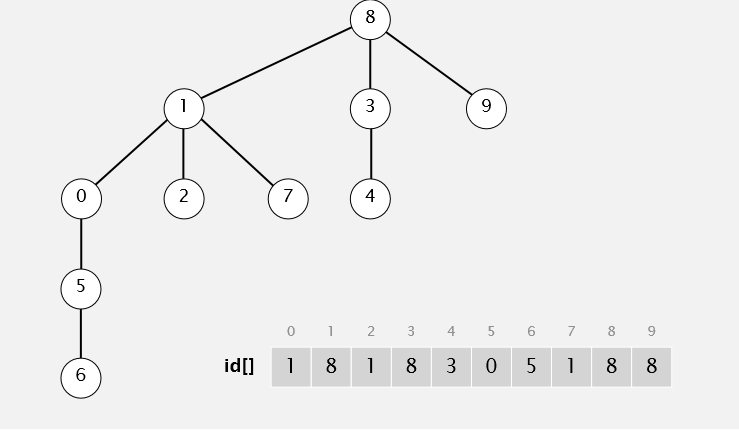
多一个测试union: ,(7,3). Quick Union 结果:
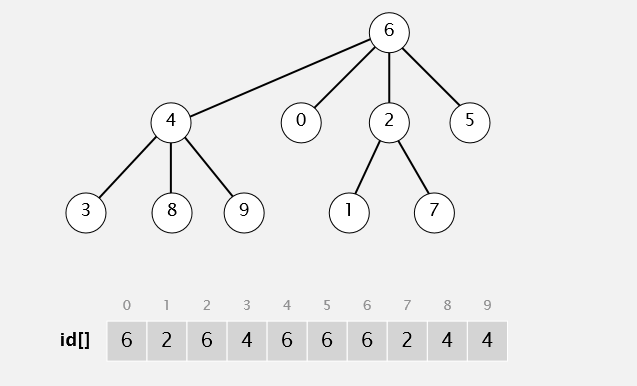
多一个测试union: ,(7,3). Quick Union+ Weight结果:
C++ 玫举与玫举类:
普通玫举是以(int)值进行比较,而玫举类可以根据不同名字来避免相同:
enum Color { red, green, blue }; enum Card { red_card, green_card, yellow_card }; enum class Animal { dog, deer, cat, bird, human }; enum class Mammal { kangaroo, deer, human }; void fun () Color color = Color::red; Card card = Card::green_card; int num = color; if (color == Card::red_card) cout << "bad" << endl; if (card == Color::green) cout << "bad" << endl; Animal a = Animal::deer; Mammal m = Mammal::deer; int num2 = a; if (m == a) cout << "bad" << endl; if (a == Mammal::deer) cout << "bad" << endl; }
希尔排序
选用Knuth的一增量序列 3X+1
先排大段,再排小段,一直到1段:
void ShellSort (int *a, int len) int isSorted = true ; for (int i = len-1 ; i > 0 ; i--) { if (a[i] < a[i - 1 ]) { SortHelper::Exch (a, i, i - 1 ); isSorted = false ; } } if (isSorted) return ; int h = 1 ; while (h <= len / 3 ) h = 3 * h + 1 ; while (h >= 1 ) { for (int i = h; i < len; i++) { for (int j = i; (j >= h) && (a[j] < a[j - h]); j -= h) { SortHelper::Exch (a, j, j - h); } } h = h / 3 ; } }
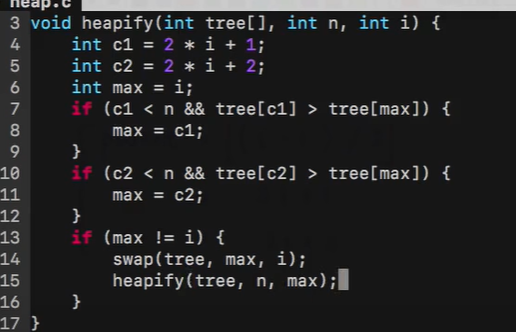
堆排序